Problemas imposibles

La t¨ªpica l¨¢mpara que se enciende y apaga desde dos interruptores (uno de los cuales es frecuente que falle, provocando un inc¨®modo ir y venir de un interruptor a otro hasta conseguir encender la luz), mencionada la semana pasada, funciona de acuerdo con el esquema de la figura.

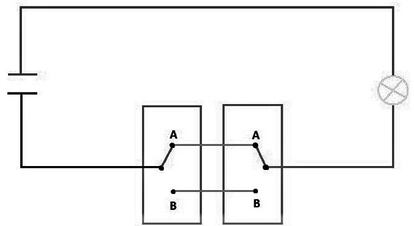
Cuando ambos interruptores hacen contacto en A, o ambos en B, se cierra el circuito y la l¨¢mpara se enciende; de lo contrario, se corta el circuito y la l¨¢mpara se apaga. (En el esquema parece todo muy sencillo; otra cosa es conectar los cables adecuadamente en una instalaci¨®n real).

Nuestro asiduo comentarista Luca Tanganelli lleva la cuesti¨®n un paso m¨¢s all¨¢ y pregunta c¨®mo ser¨ªa el circuito si una misma l¨¢mpara se encendiera y apagara desde tres interruptores. ?Y si generalizamos el problema a una l¨¢mpara con n interruptores?

En cuanto a la bombilla de interruptor desconocido, esta es la soluci¨®n de Vicente Pardo:

¡°Accionas el primer interruptor y esperas (pongamos tres minutos), lo apagas y accionas el siguiente y subes corriendo al primer piso. Tres posibilidades: la bombilla est¨¢ encendida, lo cual confirma al segundo interruptor que acabas de accionar; si la bombilla est¨¢ apagada te acercas y la tocas con la mano, si est¨¢ caliente es el primer interruptor que accionaste durante tres minutos y si est¨¢ fr¨ªa se trata del tercer interruptor¡±.

Un consejo: si esperas tres minutos, no subas corriendo o, en el caso de que el bueno fuera el primer interruptor, te quemar¨ªas la mano.

De vuelta a la geometr¨ªa

Tras unas cuantas semanas deambulando por la f¨ªsica y sus aleda?os, y antes de que se solivianten los puristas que insisten en que esta es una secci¨®n de matem¨¢ticas, volvamos a la geometr¨ªa con un par de problemas que parecen imposibles de resolver, uno por falta de datos y el otro por exceso.

El primero apareci¨® en la maravillosa secci¨®n de matem¨¢tica recreativa de Martin Gardner en Scientific American:

Dividir un tri¨¢ngulo obtus¨¢ngulo en tri¨¢ngulos acut¨¢ngulos o demostrar que es imposible.

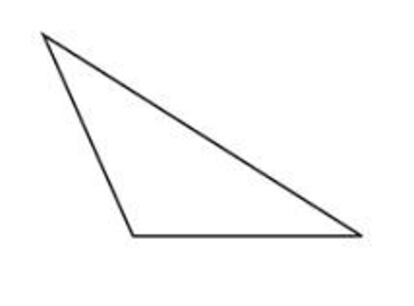
El segundo lo vi en uno de los muy recomendables libros de Clifford Pickover (no recuerdo en cu¨¢l; tal vez alg¨²n lector lo sepa) y aunque en su versi¨®n original ten¨ªa que ver con una astronave esf¨¦rica y un alien¨ªgena con tent¨¢culos, en resumen, dice as¨ª:

La superficie de una esfera y su volumen son ambos n¨²meros enteros de cuatro cifras multiplicados por ¦Ð. ?Cu¨¢l es el radio de la esfera?

Y ya que tenemos una esfera a mano, imaginemos que est¨¢ llena de un gas cuyas mol¨¦culas se agitan en su interior. ?Existir¨¢ en todo momento un plano que corte la esfera de modo que haya el mismo n¨²mero de mol¨¦culas a cada lado de este? (Se supone que el n¨²mero de mol¨¦culas en el interior de la esfera es par, claro).

Por cierto,esta entrega de El juego de la ciencia se publica el 12 11 21. ?Qu¨¦ pueden decir mis sagaces lectoras/es del elegante pal¨ªndromo 121121?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.