Sangaku

Es f¨¢cil demostrar, como se ped¨ªa la semana pasada, que 42 es la constante m¨¢gica (CM) de un cubo m¨¢gico de 3x3x3 en cuyas celdillas se colocan los n¨²meros del 1 al 27 de forma que todas las filas y columnas, as¨ª como las diagonales que pasan por el centro, sumen lo mismo, pues 1 + 2 + 3¡­ + 25 + 26 + 27 = 378, y puesto que podemos dividir el cubo en 9 columnas y todas han de sumar lo mismo, CM = 378/9 = 42.

Los n¨²meros para situar en las 27 casillas no tienen por qu¨¦ ser del 1 al 27, por lo que invito a mis sagaces lectoras y lectores a ponerse las gafas 3D e investigar otras posibilidades y caracter¨ªsticas del cubo m¨¢gico de orden 3.

O de orden 4, 5¡­

?De cu¨¢ntas maneras distintas podemos dividir un cuadril¨¢tero en tri¨¢ngulos mediante diagonales que no se corten? De dos, obviamente: uniendo uno u otro par de v¨¦rtices opuestos. ?Y un pent¨¢gono? De cinco, pues desde cada v¨¦rtice podemos trazar dos diagonales uni¨¦ndolo con los v¨¦rtices no contiguos, dividiendo de este modo el pent¨¢gono en tres tri¨¢ngulos. ?Y un hex¨¢gono? La respuesta est¨¢ impl¨ªcita en los comentarios sobre el ¡°aburrido¡± n¨²mero 42 del art¨ªculo de la semana pasada, pero os invito a buscarla sin recurrir a esa cercana ayuda.

Si las diagonales pueden cruzarse, aumenta considerablemente el n¨²mero de tri¨¢ngulos en que se puede dividir un pol¨ªgono. As¨ª, trazando las dos diagonales de un cuadril¨¢tero lo dividimos en cuatro tri¨¢ngulos. ?Cu¨¢l es el m¨¢ximo n¨²mero de tri¨¢ngulos en que podemos dividir un pent¨¢gono trazando sus diagonales? ?Y un hex¨¢gono? ?Var¨ªa dicho n¨²mero m¨¢ximo si los pol¨ªgonos son o no regulares, y si son o no convexos?

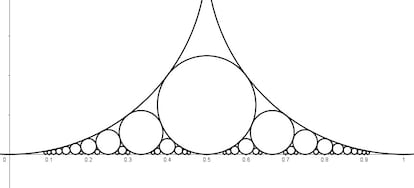
C¨ªrculos de Ford

Trazamos dos circunferencia de radio unidad tangentes entre s¨ª y tangentes ambas a una recta, y luego una tercera circunferencia tangente a las dos anteriores y a la recta. ?Cu¨¢nto mide el radio de esta tercera circunferencia?

Si seguimos trazando circunferencias ¡ªcada vez menores¡ª tangentes a la recta y a las sucesivas circunferencias, como en un tamiz de Apolonio en el que una de sus tres circunferencias generatrices tiene radio infinito (la recta), obtenemos una familia de c¨ªrculos de Ford.

La definici¨®n matem¨¢tica de c¨ªrculo de Ford puede resultar un tanto disuasoria para quienes tienen fobia a las f¨®rmulas, pero la idea es m¨¢s sencilla de lo que parece a primera vista. Un c¨ªrculo de Ford es aquel que, en unos ejes de coordenadas, tiene el centro en el punto (p/q, 1/2q 2 ) y cuyo radio es 1/2q 2 , donde p y q son n¨²meros enteros primos entre s¨ª (o, dicho de otro modo, donde p/q es una fracci¨®n irreducible). Como el radio del c¨ªrculo es igual a la ordenada del centro, los c¨ªrculos de Ford, en su representaci¨®n habitual, son tangente al eje de las abscisas, es decir, a una recta horizontal.

Los c¨ªrculos de Ford, denominados as¨ª en honor del matem¨¢tico estadounidense Lester R. Ford, que los estudi¨® en la primera mitad del siglo XX, presentan interesantes propiedades que veremos en otra ocasi¨®n; de momento, b¨¢stenos saber que algunos precedentes aparecen en los sangaku japoneses, rompecabezas geom¨¦tricos grabados en tablillas de madera que se depositaban en los templos como ofrendas a los dioses y retos a los visitantes.

En un sangaku del siglo XIX se ven tres c¨ªrculos de distintos tama?os tangentes entre s¨ª y tangentes los tres a una recta, y se pide el radio del menor conociendo los radios de los otros dos. ?Pueden mis sagaces lectoras y lectores hallar una terna de c¨ªrculos que cumplan esta condici¨®n y cuyos radios sea n¨²meros enteros?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.