El sistema di¨¦drico

Nuestro comentarista hist¨®rico Francisco Montesinos, que por un problema t¨¦cnico hab¨ªa quedado marginado de la secci¨®n de comentarios durante un tiempo, vuelve con una demostraci¨®n del teorema de Napole¨®n, del que habl¨¢bamos la semana pasada:

¡°Sea ABC un tri¨¢ngulo cualquiera, D, E, F los terceros v¨¦rtices de los tri¨¢ngulos equil¨¢teros construidos respectivamente sobre cada lado y M, N, P sus centros respectivos. Como M = A + D + B/3, N = B + E + C/3 y P = A + C + F/3 es f¨¢cil ver con algo de paciencia que (P ¨C M)e^i(pi/3) = N ¨C M, lo cual demuestra el teorema. Para demostrar la segunda parte basta observar que M + N + P = A + B + C y dividir por 3 ambos t¨¦rminos, lo cual es consecuencia inmediata de que tambi¨¦n E + F + D = A + B + C. Yo me he situado en un plano af¨ªn, que como se sabe es un espacio de puntos del plano asociado a un espacio vectorial. Aunque la belleza de la demostraci¨®n geom¨¦trica del teorema es inigualable, esta que propongo creo que no le va muy a la zaga por su alcance dentro de su simplicidad¡±.

El sistema Monge

Adelaida L¨®pez se?al¨® oportunamente que entre los matem¨¢ticos con los que se relacionaba Napole¨®n no se puede dejar de mencionar a Gaspard Monge, uno de los padres de la geometr¨ªa descriptiva y creador del sistema di¨¦drico (tambi¨¦n conocido, en su honor, como sistema Monge), que desarroll¨® en su influyente libro G¨¦ometrie descriptive, publicado en 1799. Monge tambi¨¦n es conocido, sobre todo entre los economistas, por sus importantes contribuciones a la resoluci¨®n de problemas de optimizaci¨®n (pero ese es otro art¨ªculo).

El sistema di¨¦drico, fundamental en el dibujo t¨¦cnico, consiste en representar un objeto tridimensional mediante sus proyecciones ortogonales sobre planos que se cortan perpendicularmente. Normalmente, se muestran el alzado o vista fontal, la planta o vista cenital y el perfil o vista lateral, aunque a veces basta con dos vistas (los temibles ¡°monos¡± de los ex¨¢menes de ingenier¨ªa). Invito a mis sagaces lectoras/es a reconstruir mentalmente (o con l¨¢piz y papel) los objetos cuyas proyecciones ortogonales se muestran a continuaci¨®n (las l¨ªneas de puntos representan aristas ocultas).

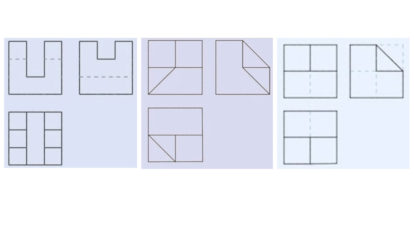
Y, para nota, un ¡°mono oral¡± (la sencilla descripci¨®n hace innecesario el dibujo) tomado de un examen de hace sesenta a?os de la Escuela de Ingenieros Industriales de Madrid:

El alzado (vista frontal) de un objeto es un c¨ªrculo, y su planta (vista cenital) es un cuadrado de lado igual al di¨¢metro del c¨ªrculo con sus dos diagonales. ?Qu¨¦ objeto es?

La retirada de Napole¨®n

Es bien sabido que una partida de ajedrez es la esquematizaci¨®n de una batalla; pero en el caso del final art¨ªstico de la semana pasada, el autor va un paso m¨¢s all¨¢, pues representa una contienda real. El rey negro es Napole¨®n. La casilla b1 es Mosc¨². La diagonal h1-a8 es el r¨ªo Ber¨¦zina. La casilla h8 es Par¨ªs. Los caballos blancos representan la caballer¨ªa cosaca. La dama en h1 es el mariscal Mija¨ªl Ilari¨®novich Golen¨ªshchev-Kut¨²zov. El rey blanco es el zar Alejandro I. Y hay un mate en 14 jugadas que se corresponden con las 14 jornadas de la retirada de Napole¨®n hasta llegar a Par¨ªs:

1. Cd2+, Ra2

2. Cc3+, Ra3

3. Cdb1+, Rb4

4. Ca2+, Rb5

5. Ca3+, Ra6

6. Cb4+, Ra7

7. Cb5+, Rb8

8. Ca6+, Rc8

9. Ca7+, Rd7

10. Cb8+, Re7

11. Cc8+, Rf8

12. Cd7+, Rg8

13. Ce7+, Rh8

14. Rg2++

Las blancas pueden dar mate en menos jugadas (?c¨®mo?), pero de este modo solo utilizan la caballer¨ªa y rinden homenaje a la memorable victoria rusa de 1812 en 14 jornadas.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.