La regularidad del 500 y el 2025

Dividir un queso de Camembert discoidal en ocho partes iguales con tres cortes rectos es sencillo¡­ si se tiene en cuenta la tercera dimensi¨®n, es decir, la altura del queso. La dificultad (psicol¨®gica m¨¢s que geom¨¦trica) de este problema estriba en que tendemos a pensar solo en cortes verticales, y en este caso la soluci¨®n cosiste en trocear el queso mediante dos cortes verticales diametrales y perpendiculares entre s¨ª, m¨¢s un tercer corte horizontal equidistante de las bases.

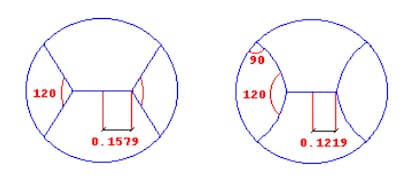
El otro problema c¨¢seo de la semana pasada no es tan sencillo. Llamando n al n¨²mero de porciones, para n = 2 y n = 3 las soluciones son triviales: en el primer caso haremos un corte diametral, y en el segundo dividiremos el queso en tres sectores de 120?. Reproduzco a continuaci¨®n la soluci¨®n dada en su d¨ªa por el autor del problema, Josep Maria Albaig¨¨s, para n = 4, incluida la ilustraci¨®n original, tomada de la revista Carrollia:

¡°Para n = 4 la cosa comienza ya a complicarse. Pues un corte seg¨²n cuatro sectores de 90 grados arrojar¨ªa una longitud de corte L = 4, mientras que en el sistema indicado en la figura de la izquierda basta con L = 3,9624. Esta divisi¨®n se ha obtenido recordando la conocida propiedad de que el punto situado en el interior de un tri¨¢ngulo cuya suma de distancias a los tres v¨¦rtices es m¨ªnima es el que ve estos bajo ¨¢ngulos de 120 grados. Sin embargo, todav¨ªa puede mejorarse: intuitivamente se comprende que, al no ser los segmentos rectos incidentes sobre la circunferencia perpendiculares a esta podr¨ªan ser sustituidos por arcos de circunferencia que cumplieran con esta condici¨®n. Se mejora todav¨ªa algo, llegando a la figura de la derecha donde L = 3,9412¡å.

N¨²meros regulares

Adem¨¢s de ser la primera de 2025, esta es la entrega no. 500 de El juego de la ciencia, y aunque no hay que sobrevalorar los n¨²meros redondos, uno tan redondo como este, que en la numeraci¨®n romana merec¨ªa letra propia, no puede pasar inadvertido.

Am¨¦n de su doble redondez (pues termina en dos ceros), la peculiaridad matem¨¢tica m¨¢s destacable del 500 es que se trata de un n¨²mero regular. N¨²meros regulares son aquellos entre cuyos factores primos no hay ninguno mayor que 5 (es decir, solo 2, 3 y 5), y fueron de gran importancia entre los babilonios (?adivinas ¡ªmejor dicho, deduces¡ª por qu¨¦?); los veinte primeros son:

1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36¡­

Se incluye el 1 porque seg¨²n otra definici¨®n (la primera, en realidad) n¨²mero regular es el que divide a alguna potencia de 60 (y por ende de 30).

Fuera del ¨¢mbito de las matem¨¢ticas, el 500 da nombre a un juego de cartas de pujas y por parejas similar al bridge (en el que los jugadores declaran de antemano el n¨²mero de bazas que esperan ganar). En una de las variantes hay que obtener exactamente 500 puntos, de ah¨ª el nombre del juego.

Por cierto, 2025 tambi¨¦n es un n¨²mero regular, adem¨¢s de un cuadrado perfecto (452). Y puesto que tanto 500 como el a?o en el que entramos son divisibles por 5, hagamos que tambi¨¦n lo sea un cuadrado. Es muy f¨¢cil dividir un cuadrado en 4 cuadrados iguales, pero no tanto en 5, aunque se puede conseguir mediante una construcci¨®n geom¨¦trica relativamente sencilla. ?Puedes dividir un cuadrado en 5 cuadrados iguales sin m¨¢s ayuda que la de una regla? Y si recurres a la papiroflexia, ni siquiera es necesario que est¨¦ graduada.

Y, para terminar, no puede faltar un problemilla relacionado con el nuevo a?o:

Por Navidad me han regalado dos agendas diarias de 2025, y como solo necesito una, guardo la otra para el pr¨®ximo a?o que empiece en mi¨¦rcoles (y no sea bisiesto). ?Cu¨¢nto me falta para estrenarla?

Un nuevo a?o y 500 entregas de El juego de la ciencia: doble motivo para agradecerles a mis lectoras y lectores habituales su regularidad y sus sagaces comentarios, que hacen que esta columna sea algo m¨¢s que una mera secci¨®n de pasatiempos matem¨¢ticos.