El teorema de Van Aubel

En el a?o 2011, la Real Sociedad Matem¨¢tica Espa?ola cumpl¨ªa 100 a?os. Para celebrar este centenario, la RSME program¨® una buena cantidad de actividades, entre las que estaba la propuesta de cuarenta desaf¨ªos matem¨¢ticos, en colaboraci¨®n con El Pa¨ªs, con sorteos de colecciones de libros de matem¨¢ticas entre las personas que consiguieran resolver cada uno de ellos. De hecho, se siguen proponiendo desaf¨ªos especiales algunos veranos y, sobre todo, en Navidad.

Estos desaf¨ªos trataron diversas ramas de las matem¨¢ticas (teor¨ªa de n¨²meros, geometr¨ªa, probabilidad¡­), y fueron presentados principalmente por matem¨¢ticos de toda la geograf¨ªa espa?ola. De hecho, el que escribe estas l¨ªneas tuvo el gran honor de proponer uno de ellos, concretamente el que hac¨ªa el n¨²mero 39.

El m¨ªo fue un desaf¨ªo geom¨¦trico que involucraba tri¨¢ngulos, cuadrados, distancias y ¨¢ngulos. Y no es de extra?ar, ya que los que pas¨¢is habitualmente por aqu¨ª sab¨¦is que me gusta mucho la geometr¨ªa. V¨¦anse, por ejemplo, el art¨ªculo sobre la circunferencia de Feuerbach, el de la f¨®rmula de Euler, el del centro del tri¨¢ngulo o el de las l¨ªneas con nombre.

Volviendo a mi desaf¨ªo (por cierto, aqu¨ª os dejo la propuesta del mismo y la soluci¨®n), quer¨ªa hablar hoy del resultado matem¨¢tico que lo motiv¨®. Dicho resultado es un teorema geom¨¦trico muy bonito pero no demasiado conocido que responde al nombre de teorema de Van Aubel, en honor al matem¨¢tico holand¨¦s Henri Van Aubel.

Este teorema nos dice lo siguiente:

Lo m¨¢s sorprendente de este teorema es que, como puede leerse en el enunciado, es v¨¢lido para cualquier cuadril¨¢tero. S¨ª, s¨ª, cualquiera. Se cumple para cuadril¨¢teros convexos, como el de la siguiente imagen:

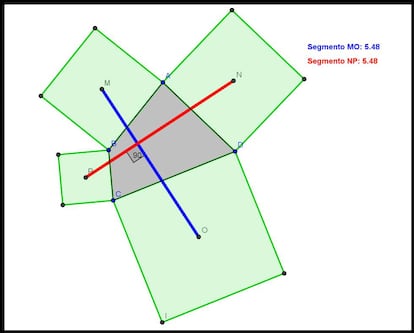
Pero tambi¨¦n se cumple para cuadril¨¢teros no convexos, como podemos ver en la figura siguiente:

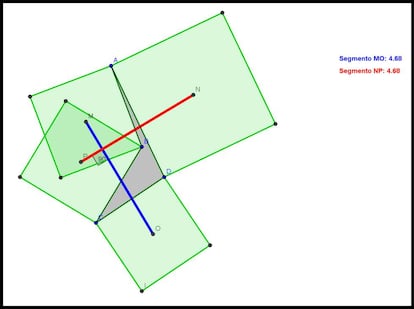
E, incluso, para cuadril¨¢teros en los que hay intersecciones entre sus lados. A continuaci¨®n pod¨¦is ver un ejemplo:

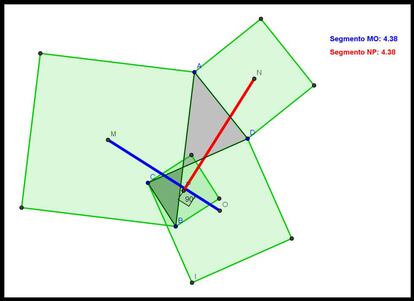
Y, por si fuera poco, si los cuadrados que dibujamos son ¡°internos¡± en vez de ¡°externos¡±, el teorema se sigue cumpliendo. Vamos, un teorema de esos que nos gustan, de los que con poquito que les demos nos lo ofrecen todo, de los que necesitan poco para mostrarnos toda su belleza.

Las im¨¢genes que os he mostrado antes son muy buenas para apreciar la maravilla de teorema que tenemos delante, pero la realidad es que son im¨¢genes est¨¢ticas de casos concretos. Os podr¨ªa haber ense?ado con ellas algunos casos particulares en los que el teorema s¨ª se cumpliera, pero no podr¨ªamos ver qu¨¦ ocurre con otros cuadril¨¢teros. Por ello, como suelo hacer en art¨ªculos de geometr¨ªa plana como este, os dejo a continuaci¨®n un applet de GeoGebra con el que pod¨¦is jugar con los v¨¦rtices del cuadril¨¢tero inicial (A, B, C y D) y comprobar, ahora s¨ª, que los segmentos citados en el teorema (MO y NP) miden lo mismo y son perpendiculares:

Con este applet interactivo muchos se habr¨¢n convencido de la veracidad del teorema de Van Aubel, pero seguro que muchos otros (y con mucha raz¨®n) necesitan de una demostraci¨®n para tener claro que el teorema es cierto. Pues, a pesar de la fuerza (da igual c¨®mo sea el cuadril¨¢tero inicial) y la belleza del resultado, no es muy complicado demostrarlo.

Os animo a intentarlo vosotros mismos, y para ello os dejo una sugerencia que os puede ayudar a ello: utilizar el resultado que yo demostr¨¦ en el desaf¨ªo 39 puede ser interesante. Si ten¨¦is alguna duda, o si quer¨¦is mostrarnos vuestros progresos, pod¨¦is usar los comentarios para hablarnos sobre ello.

La geometr¨ªa es una de las ramas de la ciencia m¨¢s olvidadas en la educaci¨®n secundaria. Muchos teoremas geom¨¦tricos maravillosos que se estudiaban en otras ¨¦pocas en esta etapa ya han desaparecido del curr¨ªculo, por lo que los estudiantes de la actualidad se est¨¢n perdiendo aut¨¦nticas maravillas matem¨¢ticas. Estar¨ªa bien que les echarais una mano habl¨¢ndoles, en los comentarios de este art¨ªculo, sobre otros teoremas geom¨¦tricos que os parezcan dignos de ser recordados. Muchas gracias.