Una original manera de celebrar el d¨ªa de Pi

M¨¢s informaci¨®n

D¨ªa de Pi: los algoritmos permiten obtener nuevas cifras de ¦Ð

Hoy, d¨ªa 14 de marzo, es el d¨ªa en el que, en todas las partes del mundo, se homenajea al que es posiblemente el n¨²mero real m¨¢s citado en toda la historia de las matem¨¢ticas. Hoy, 14 de marzo, es el d¨ªa de Pi. Y lo es porque, escrito en notaci¨®n estadounidense, el d¨ªa de hoy es 3-14, que corresponde con una aproximaci¨®n de Pi a dos decimales.

Como decimos, esta convocatoria de celebraci¨®n anual del d¨ªa de Pi se hace a nivel mundial, y son muchas las actividades que se realizan gracias a ellas: se programan conferencias sobre Pi, se convocan concurso de relatos y audiovisuales con Pi como protagonista, se realizan publicaciones relacionadas con Pi en multitud de redes sociales, se escriben art¨ªculos relacionados con Pi (como este), etc¨¦tera. Por poner un ejemplo patrio, desde el a?o pasado en Espa?a tenemos la iniciativa Sin Pi no soy nada, impulsada por varias instituciones, que organiza distintos tipos de actividades relacionadas con Pi.

Lo que os voy a contar hoy sobre Pi, este n¨²mero conocido principalmente por ser la raz¨®n entre la longitud de una circunferencia y su di¨¢metro, es una sencilla manera de calcular una aproximaci¨®n suya en casa y utilizando instrumentos que todos tenemos a mano. Y quiz¨¢s lo m¨¢s curioso de la misma es que no tiene nada que ver con circunferencias, que es lo que uno habr¨ªa esperado sabiendo la relaci¨®n tan ¨ªntima que tiene este n¨²mero Pi con las cosas redondas. En realidad, el tema va de rectas y probabilidad.

Pero antes vamos con un poquito de historia, que la cuesti¨®n que estamos tratando tiene ya un tiempo. Corr¨ªa el a?o 1733 cuando el naturalista franc¨¦s Georges Luis Leclerc, m¨¢s conocido como conde de Buffon, se plantea el siguiente problema:

¡°Dibujamos en el suelo (nos valdr¨ªa cualquier superficie plana) l¨ªneas rectas paralelas tal que la distancia entre cada dos consecutivas sea siempre la misma. Ahora, tiramos al azar una aguja en ese suelo. ?Cu¨¢l es la probabilidad de que esa aguja corte a alguna de las l¨ªneas?¡±

Como veis, no aparecen circunferencias por ning¨²n lado, solamente l¨ªneas rectas y el c¨¢lculo de cierta probabilidad.

El propio Buffon resolvi¨® el problema en 1757, y en dicha resoluci¨®n se aprecia que el resultado depende de la longitud de la aguja que lanzamos (algo que, por otra parte, parec¨ªa evidente). Nosotros nos vamos a quedar con el caso m¨¢s sencillo: vamos a tirar una aguja que mide lo mismo que la distancia entre dos l¨ªneas consecutivas. En la siguiente imagen pod¨¦is ver los, esencialmente, dos ¨²nicos casos que se nos pueden dar:

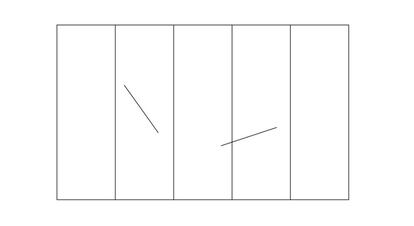
Bien, pues en esta situaci¨®n Buffon demostr¨® que la probabilidad de que esa aguja corte a alguna de las l¨ªneas es 2/¦Ð. S¨ª, otra situaci¨®n en la que el n¨²mero Pi aparece de manera sorpresiva e inesperada y que, probablemente, ni siquiera el propio Buffon esperaba.

Veamos ahora c¨®mo podemos usar esto para realizar en casa (o con amigos, alumnos¡­) una actividad de celebraci¨®n del d¨ªa de Pi. Tomemos boli, papel, regla y una aguja. Dibujamos unas l¨ªneas rectas en el papel distanciadas la misma longitud, como hemos comentado, y comencemos a dejar caer la aguja de manera azarosa.

Tenemos que contar cu¨¢ntos lanzamientos hacemos, digamos N, y cu¨¢ntos de ellos cortan a alguna de las l¨ªneas, pongamos C. Con estos datos, la probabilidad de que la aguja corte a alguna l¨ªnea en ese n¨²mero de lanzamientos se puede calcular dividiendo el n¨²mero de casos favorables, C, entre el n¨²mero de casos total, N. Por tanto, esa divisi¨®n ser¨¢ una aproximaci¨®n de la probabilidad que Buffon nos calcul¨®, por lo que C/N ¡Ö 2/¦Ð. Despejando Pi de ah¨ª tenemos que:

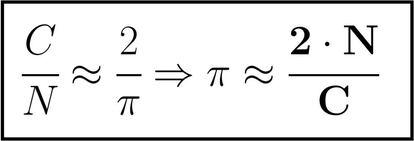
Esto es, en este experimento, llamado aguja de Buffon, podemos calcular una aproximaci¨®n de Pi multiplicando por 2 el n¨²mero de lanzamientos y dividiendo despu¨¦s entre el n¨²mero de cortes obtenidos. ?No os parece maravilloso?

Pero, por desgracia, no todo es tan bonito como parece. Aunque como actividad es bastante curiosa y puede ser muy interesante, meti¨¦ndonos ya un poco m¨¢s en las matem¨¢ticas del m¨¦todo nos encontramos con un gran problema pr¨¢ctico: para encontrar una buena aproximaci¨®n de Pi mediante el m¨¦todo de la aguja de Buffon tendr¨ªamos que realizar una cantidad enoooooorme de lanzamientos (dicho de forma m¨¢s matem¨¢tica, la convergencia del m¨¦todo es lent¨ªsima).

Si hac¨¦is pruebas en casa, como ya os he sugerido, os dar¨¦is cuenta de ello. Pero tambi¨¦n pod¨¦is verlo en Buffon¡¯s Needle, an analysis and simulation, un simulador de la aguja de Buffon que tienen en la web de la Universidad de Illinois. Ah¨ª pod¨¦is realizar tiradas simuladas de aguja y ver qu¨¦ aproximaci¨®n obtenemos. Yo acabo de hacer cinco pruebas distintas de 100.000 tiradas cada una y las aproximaciones obtenidas han sido las siguientes (os las redondeo a cuatro decimales):

3.1344, 3.1369, 3.1362, 3.1392, 3.1431

Es decir, solamente en una de ellas obtenemos el segundo decimal exacto, y eso tirando la aguja nada menos que 100.000 veces. Curioso e interesante, pero poco ¨²til matem¨¢ticamente hablando, lamentablemente. De todas formas, espero que este peque?o contratiempo no rebaje la euforia que, muy posiblemente, se haya desatado en vuestras mentes despu¨¦s de conocer este maravilloso m¨¦todo de la aguja de Buffon.

Para terminar, un apunte relacionado con la longitud de la aguja. Hemos tratado el caso en el que esta longitud es igual que la distancia entre l¨ªneas, pero tambi¨¦n podemos considerar otras situaciones.

Supongamos que la aguja mide L y la distancia entre rectas es D. Si la aguja es m¨¢s corta (es decir, L < D), tenemos que la probabilidad de que la aguja corte a alguna recta es 2L/D¦Ð; si la aguja es m¨¢s larga (esto es, L > D), el valor de dicha probabilidad se complica bastante. Quienes est¨¦is interesados en los desarrollos matem¨¢ticos que nos calculan todas estas probabilidades pod¨¦is encontrar informaci¨®n al respecto en el siguiente pdf: Buffon¡¯s Needle Problem.