D¨ªa de Pi: los algoritmos permiten obtener nuevas cifras de ¦Ð

M¨¢s informaci¨®n

Desaf¨ªo matem¨¢tico | M¨²ltiplos del n¨²mero Pi que pretenden ser enteros

Muere el f¨ªsico Stephen Hawking a los 76 a?os

El n¨²mero Pi sigue encerrando misterios que los matem¨¢ticos de todo el mundo tratan de resolver. Por ejemplo, todav¨ªa no se sabe si es un n¨²mero normal en base 10, es decir si contiene en su desarrollo decimal cualquier sucesi¨®n finita de d¨ªgitos con la frecuencia que sugiere su tama?o. Una manera de investigar esta caracter¨ªstica es hacer estudios estad¨ªsticos en los millones de cifras decimales conocidas del n¨²mero. Para ello, es necesario computar una cantidad cada vez mayor de d¨ªgitos de Pi.

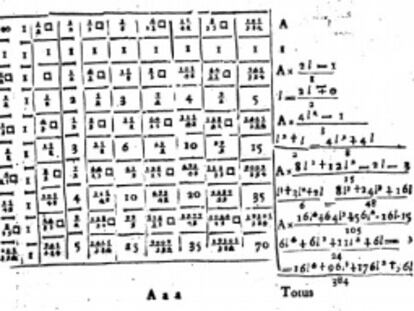
Esto se consigue gracias a los algoritmos que idean los matem¨¢ticos en base a las f¨®rmulas de la teor¨ªa de n¨²meros en las que aparece Pi. Los m¨¢s empleados son los algoritmos iterativos y las series. Un algoritmo iterativo est¨¢ formado por unos valores iniciales y una lista finita de operaciones que hay que realizar de forma c¨ªclica una y otra vez de manera que en cada iteraci¨®n va mejorando el resultado y, en este caso, permite obtener m¨¢s cifras de Pi. Cuanto m¨¢s mejore el resultado en cada iteraci¨®n, y m¨¢s sencillas sean las operaciones que involucra, mejor ser¨¢ el algoritmo. Por otro lado, una serie es una suma infinita de t¨¦rminos, y se aproxima mediante una suma finita; cuantos m¨¢s sumandos de la serie se consideren, mejor ser¨¢ la aproximaci¨®n.

Hasta hace unos pocos a?os los r¨¦cords de n¨²mero de cifras se bat¨ªan con superordenadores, pero el ¨²ltimo (de m¨¢s de 22 billones de cifras decimales), se ha conseguido usando un programa, ideado por el ingeniero de software Alexander Yee, que se puede descargar en ordenadores personales. Para llegar a esta situaci¨®n han transcurrido muchos a?os de historia de f¨®rmulas, cada vez m¨¢s eficientes.

M¨¢s informaci¨®n

(Creemos que) Todos los n¨²meros est¨¢n en Pi

Hasta mediados del siglo XVII el ¨²nico m¨¦todo disponible (salvo variantes) era el ideado por Arqu¨ªmedes de Siracusa, aproximadamente el a?o 250 a.C. Consist¨ªa en considerar un hex¨¢gono inscrito y otro circunscrito a una circunferencia de di¨¢metro unidad, y duplicar una y otra vez el n¨²mero de lados para aproximar ¦Ð con los per¨ªmetros de los sucesivos pol¨ªgonos.

El c¨¢lculo infinitesimal del siglo XVII propici¨® la obtenci¨®n de algoritmos mucho m¨¢s eficientes, entre los que destaca el del ingl¨¦s John Machin, basado en la identidad ¦Ð = 16 arctan(1/5) - 4 arctan(1/239) y en la por entonces bien conocida serie para el arco tangente (arctan x). Machin pudo obtener f¨¢cilmente 100 d¨ªgitos de Pi con esta f¨®rmula. Otras similares, pero m¨¢s eficientes, siguen estando entre las m¨¢s empleadas hoy en d¨ªa.

Leonhard Euler tambi¨¦n se sinti¨® fascinado por la famosa constante, y en 1748 logr¨® representar ¦Ð como producto de dos integrales el¨ªpticas. Carl Friedrich Gauss utiliz¨® este resultado en el a?o 1800 para demostrar una f¨®rmula que duplica en cada iteraci¨®n el n¨²mero de decimales correctos. Pero las operaciones de este algoritmo involucran ra¨ªces y resultan tediosas si se efect¨²an a mano. Gauss no se molest¨® en hacerlas y la f¨®rmula se olvid¨® hasta que fue redescubierta en 1970 y de forma independiente por los matem¨¢ticos E. Salamin y R. Brent.

M¨¢s informaci¨®n

Cuando pol¨ªticos de EE UU decidieron que el n¨²mero pi era 3,2

En 1914 se public¨® un famoso art¨ªculo del matem¨¢tico indio Srinivasa Ramanujan con sorprendentes f¨®rmulas para el inverso de ¦Ð, en forma de series infinitas. En la m¨¢s espectacular, cada sumando aporta ocho d¨ªgitos correctos. En 1985 William Gosper la implement¨® con ordenador y bati¨® un r¨¦cord de m¨¢s de 17 millones de cifras de ¦Ð. Dos a?os despu¨¦s los hermanos ucranianos David y Gregory Chudnovsky obtuvieron una f¨®rmula del mismo estilo, pero todav¨ªa m¨¢s impresionante: va dando los decimales de 14 en 14. Ese mismo a?o los hermanos Jonathan y Peter Borwein obtuvieron un algoritmo cu¨¢rtico, es decir que cuadruplica en cada iteraci¨®n el n¨²mero de d¨ªgitos correctos, utilizando ecuaciones modulares de Ramanujan.

Yo tambi¨¦n me cuento entre los matem¨¢ticos fascinados con estos problemas. En los a?os 2002 y 2003 demostr¨¦ de una forma completamente diferente algunas de las series de tipo Ramanujan para el inverso de ¦Ð, usando para ello el llamado m¨¦todo WZ. Estas investigaciones tambi¨¦n me condujeron a un nuevo tipo de f¨®rmulas, de aspecto parecido a las de Ramanujan pero para el inverso del cuadrado de ¦Ð.

M¨¢s informaci¨®n

Una original manera de celebrar el d¨ªa de Pi

Mis f¨®rmulas, aunque de convergencia r¨¢pida, no se encuentran entre las que sirven para batir r¨¦cords, pero plantean nuevos e interesantes retos a los matem¨¢ticos. Por un lado, no se dispone a¨²n de una teor¨ªa que permita entenderlas en profundidad, y por otro, muchas de ellas siguen sin haberse podido demostrar todav¨ªa aunque hay evidencia num¨¦rica de que tienen que ser ciertas.

Jes¨²s Guillera est¨¢ jubilado y es colaborador extraordinario de la Universidad de Zaragoza.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.