El problema de distinguir dos f¨®rmulas qu¨ªmicas iguales

En matem¨¢ticas y en qu¨ªmica se usan f¨®rmulas. Una f¨®rmula matem¨¢tica relaciona constantes y variables a trav¨¦s de una igualdad; mientras que una qu¨ªmica, busca determinar un compuesto a partir de los ¨¢tomos que contiene y la proporci¨®n en la que ¨¦stos aparecen. El gran problema radica en que distintas sustancias pueden tener la misma f¨®rmula qu¨ªmica, como observ¨® en 1811 Joseph Louis Gay-Lussac. ?Vaya! Esta f¨®rmula, entonces, no parece demasiado ¨²til. En 1823, el qu¨ªmico Justus von Liebig demostr¨® que el fulminato de plata y el cianato de plata, ambos formados por mol¨¦culas que conten¨ªan un ¨¢tomo de plata, uno de carbono, uno de ox¨ªgeno y otro de nitr¨®geno, ten¨ªan propiedades muy distintas: en particular, el primero era muy explosivo y el segundo no. Si sus mol¨¦culas constaban de los mismos ¨¢tomos y en la misma cantidad, la diferencia entre ambos ten¨ªa que residir necesariamente en la manera en que esos ¨¢tomos se enlazaban en cada mol¨¦cula. Gay-Lussac comunic¨® estos estudios al tambi¨¦n qu¨ªmico J?ns Jacob von Berzelius. De hecho, este ¨²ltimo ya hab¨ªa observado un fen¨®meno similar: hab¨ªa descubierto que el ¨¢cido rac¨¦mico y el ¨¢cido tart¨¢rico parec¨ªan tener la misma f¨®rmula emp¨ªrica (G4H6O6) pero no compart¨ªan las mismas propiedades.

Berzelius sugiri¨® denominarlos is¨®meros. Es decir, dos compuestos qu¨ªmicos se llaman is¨®meros si poseen la misma f¨®rmula qu¨ªmica (mismas proporciones relativas de los ¨¢tomos que componen sus mol¨¦culas) pero con diferentes estructuras qu¨ªmicas (maneras en que sus ¨¢tomos se enlazan) y, por lo tanto, diferentes propiedades y configuraci¨®n.

En 1875, el matem¨¢tico Arthur Cayley, notable pol¨ªmata e interesado desde joven por la qu¨ªmica, se enter¨® del problema de la enumeraci¨®n de los is¨®meros a trav¨¦s de su amigo, el qu¨ªmico alem¨¢n Carl Schorlemmer. Cayley decidi¨® utilizar sus conocimientos sobre la teor¨ªa de grafos para enumerar todas las posibles configuraciones de los is¨®meros de los alcanos de f¨®rmula CnH2n+2. Para abordar el problema emple¨® unos objetos matem¨¢ticos llamados grafos.

Un grafo es un conjunto formado por v¨¦rtices y aristas, que representan relaciones binarias, las posibles uniones, entre los primeros. La valencia de un v¨¦rtice es el n¨²mero de aristas incidentes al v¨¦rtice. En concreto, Cayley emple¨® un cierto tipo de grafos, los llamados ¨¢rboles, aquellos en los que dos v¨¦rtices cualesquiera est¨¢n conectados por exactamente un camino de aristas.

A Cayley se le ocurri¨® que los v¨¦rtices de los ¨¢rboles pod¨ªan representar los ¨¢tomos de carbono de los alcanos (los de hidr¨®geno se pod¨ªan a?adir m¨¢s adelante) y se trataba entonces de enumerar todas las posibles configuraciones, es decir, todos los posibles enlaces entre esos v¨¦rtices. Su propuesta se basaba en el n¨²mero de centros (v¨¦rtices de valencia mayor que 1) de la f¨®rmula qu¨ªmica. Cayley demostr¨® que estos ¨¢rboles tienen siempre v¨¦rtices de valencia menor o igual a cuatro y solo pod¨ªan tener uno o dos centros.

Por ejemplo, consideremos dos is¨®meros del alcano con cinco ¨¢tomos de carbono, el pentano, de f¨®rmula C5H12. En primer lugar, el 2,2-dimetilpropano (C(CH3)4), que posee cuatro v¨¦rtices de valencia 1 y uno de valencia 4, que es por lo tanto su ¨²nico centro:

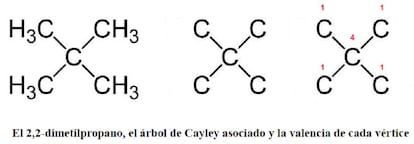
Por otro lado, el 2-metilbutano ((CH3)2-CH-CH2-CH3), que posee tres v¨¦rtices de valencia 1 y dos de valencia 2; estos dos ¨²ltimos son los centros:

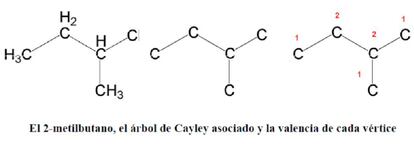
Bas¨¢ndose en las propiedades matem¨¢ticas de este tipo de ¨¢rboles, Cayley propuso una f¨®rmula para calcular el n¨²mero de is¨®meros de los alcanos CnH2n+2: su expresi¨®n era exacta para n de 1 a 11, pero fallaba m¨¢s all¨¢. Una l¨¢stima.

Tambi¨¦n invent¨® un algoritmo que permit¨ªa calcular el n¨²mero de is¨®meros para n (CnH2n+2) conociendo el n¨²mero de is¨®meros para n-1 (Cn-1H2n).

Para mostrar el inter¨¦s pr¨¢ctico de su propuesta, Cayley aplic¨® su m¨¦todo a los alcoholes de f¨®rmula CnH2n+1OH, en los que se sustitu¨ªa un ¨¢tomo de hidr¨®geno por el radical OH. Aplicaba su teor¨ªa utilizando como v¨¦rtices del ¨¢rbol los ¨¢tomos de carbono y el radical OH. Cayley calcul¨® que deb¨ªa haber ocho is¨®meros del pentanol, de f¨®rmula C5H11OH. Todos fueron identificados posteriormente (1-pentanol, 3-metil-1-butanol, 2-metil-1-butanol, 2,2-dimetil-1-propanol, 3-pentanol, 2-pentanol, 3-metil-2-butanol y 2-metil-2-butanol), confirmando el m¨¦todo de Cayley.

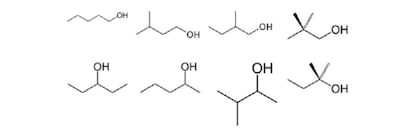
Por supuesto, existen otras maneras de clasificar los is¨®meros qu¨ªmicos (¨®pticos, estables, etc.). Pero The Online Encyclopedia of Integer Sequences ha seguido la teor¨ªa de Cayley para conocer el n¨²mero de is¨®meros de alcano. Se estima que el alcano C167H336 posee m¨¢s is¨®meros que part¨ªculas tiene el universo.

Marta Macho-Stadler es profesora del Departamento de Matem¨¢ticas de la Universidad del Pa¨ªs Vasco y miembro de la Comisi¨®n de G¨¦nero del ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n:?gata Tim¨®n (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra Newsletter.