Lo que sabemos de las superficies a trav¨¦s de sus puntos singulares

M¨¢s informaci¨®n

El domin¨® binario de Gardner

Dominar el domin¨®

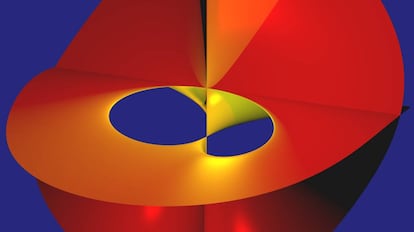
Es Miau. No es un gato, y tampoco un sacacorchos. Es una figura matem¨¢tica; en concreto, es la superficie representada por la f¨®rmula ?²??+?²?²+2?³?+3?³=0. Tres letras (estas misteriosas x, y, z del final del alfabeto), algunos n¨²meros y una igualdad. La expresi¨®n evoca interminables clases en la escuela, cuando nos abandonaban a estos s¨ªmbolos y enigmas que nos tra¨ªan de cabeza. Pero m¨¢s all¨¢ de nuestros recuerdos nost¨¢lgicos, esta combinaci¨®n de letras y n¨²meros contiene, de un modo a¨²n desconocido para el lego, toda la informaci¨®n sobre la geometr¨ªa, la curvatura, la ubicaci¨®n de las puntas y de los ejes de la figura. El campo de las matem¨¢ticas que explica esta relaci¨®n entre ecuaciones y figuras se llama geometr¨ªa algebraica. Es un campo cl¨¢sico, dif¨ªcil y muy popular en la investigaci¨®n actual. Hay todo un diccionario que hace equivaler las propiedades geom¨¦tricas de las superficies con las propiedades algebraicas de las ecuaciones correspondientes. Se pueden calcular curvaturas, puntos de intersecci¨®n, puntas, ¨¢reas, agujeros, pliegues, y muchas cosas m¨¢s. Estos objetos matem¨¢ticos configuran todo un zoo, y sobre ellos hay una teor¨ªa enormemente est¨¦tica y satisfactoria.

Pero lo cierto es que, por muy bonita que sea, a primera vista, poco podemos entender de la ecuaci¨®n anterior. Tratemos de explorarla desde el punto de vista geom¨¦trico. Quiz¨¢s merece la pena dar la vuelta al dibujo, verlo desde detr¨¢s.Parece ser que se esconde una rana que croa:

Ahora vemos un agujero (?o dos?), dos puntas que casi se tocan, una recta horizontal, y una amplia b¨®veda, con luz y color de reverberaci¨®n. La figura parece ser sim¨¦trica: la parte de izquierda es id¨¦ntica a la parte derecha, ?o no?. Desde otras perspectivas, podemos ver las figuras de abajo. Aparecen ejes de intersecci¨®n, hojas, curvaturas, cambios de orientaci¨®n. Lo cierto es que seguimos sin entender demasiado.

Dos de sus ejes son visibles en la superficie (como puede verse en las im¨¢genes 3, 4 y 5), y en ellos ¡°ocurren¡± singularidades. Estos son puntos donde la geometr¨ªa se distingue sustancialmente del resto (que se llaman puntos lisos o regulares). Son puntos muy particulares, casi extraordinarios: o bien intersecciones de hojas (horizontalmente a lo largo del eje x), o bien aristas (verticalmente a lo largo del eje z), o bien puntos a¨²n m¨¢s especiales como el espig¨®n en el punto de intersecci¨®n de los tres ejes.

En los puntos lisos de una variedad la vida es un poco aburrida: es como un llano, o una colina muy suave. En un punto singular hay sorpresas, v¨¦rtigos y rincones escondidos: la geometr¨ªa local es mucho m¨¢s rica, y su comprensi¨®n permite entender ciertos fen¨®menos ¡°catastr¨®ficos¡±. En ciencias naturales estos puntos se corresponden a c¨¢usticas en ¨®ptica, singularidades en f¨ªsica y teor¨ªa de ondas, es decir, remolinos, agujeros negros, la ruptura de una ola¡­ son aquellos sucesos en los que, de repente, se perturba la calma y aparece un desgarro. Entender c¨®mo se forman y c¨®mo evolucionan es clave para describir estos fen¨®menos.

Es por ello que los matem¨¢ticos dedican una gran cantidad de esfuerzos a responder preguntas del tipo: ?c¨®mo se forman las singularidades? ?C¨®mo se detectan en la ecuaci¨®n? Existen cuestiones infinitas sobre las singularidades, algunas est¨¢n resueltas y otras siguen siendo misterios para los matem¨¢ticos que las estudian. Uno de los resultados conocidos m¨¢s importantes es el teorema de resoluci¨®n de singularidades de variedades algebraicas (una generalizaci¨®n del concepto de superficie) en caracter¨ªstica zero, probado por el matem¨¢tico japon¨¦s Heisuke Hironaka, medalla Fields en 1970. Dice que cualquier singularidad es la sombra de una superficie lisa sin singularidades, y as¨ª permite entender matem¨¢ticamente c¨®mo nacen las singularidades. Es un resultado profundo, muy dif¨ªcil de demostrar y con much¨ªsimas aplicaciones, que nos permitir¨¢n en el futuro comprender mejor la naturaleza de algunas cat¨¢strofes.

Adem¨¢s, abre preguntas a¨²n por responder, como la llamada resoluci¨®n en caracter¨ªstica positiva, una extensi¨®n del resultado de Hironaka a variedades de caracter¨ªstica mayor que cero.Este resultado reta a grandes matem¨¢ticos desde hace m¨¢s de cincuenta a?os. Por el momento, no se sabe si es cierta o falsa, y los cient¨ªficos tienen que vivir con esta incertidumbre, este v¨¦rtigo, hasta que una de las dos opciones se haya verificado.

Herwig Hauser es profesor de la Universidad de Viena (Austria) y creador de las im¨¢genes de superficies algebraicas cl¨¢sicas IMAGINARY que ilustran este art¨ªculo.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.