Un aficionado hace el primer avance de los ¨²ltimos 60 a?os en un famoso problema de combinatoria

El llamado problema de Hadwinger-Nelson es de esas cuestiones matem¨¢ticas muy f¨¢ciles de formular y entender, incluso para los no expertos, como el problema del mapa de los cuatro colores o el ¨²ltimo teorema de Fermat. Sin embargo, pese a esta aparente sencillez a menudo la soluci¨®n resulta extraordinariamente sofisticada y requiere unas matem¨¢ticas que solo est¨¢n al alcance de muy pocos expertos. Pese a ello, el autor del primer avance en el problema de Hadwinger-Nelson de los ¨²ltimos 60 a?os ha sido un no especialista: Aubrey de Grey, un geront¨®logo bastante conocido y medi¨¢tico, que sostiene que es posible detener el proceso de envejecimiento.

El problema de Hadwiger-Nelson estudia coloraciones del plano. Se trata de dar un color a cada punto del plano de manera que todos los puntos que est¨¦n a distancia uno tengan asignado un color diferente. Si se quiere pintar de esta manera un plano, todo lo grande que queramos, ?cu¨¢l es el menor n¨²mero de colores necesarios? El problema fue planteado en 1950 por Edward Nelson, aunque algunos resultados relacionados ya aparecieron en un art¨ªculo de Hugo Hadwiger de 1945. Hasta hace poco, se sab¨ªa que la respuesta pod¨ªa ser cuatro, cinco, seis o siete.

Efectivamente, no puede ser m¨¢s de siete. Con solo siete colores se puede colorear el plano a partir de una teselaci¨®n de hex¨¢gonos de diagonal ligeramente inferior a uno, en la que todos los pol¨ªgonos adyacentes tengan un color diferente. Partimos de uno de los hex¨¢gonos y lo pintamos de un color, y los seis adyacentes de otros seis colores diferentes (y as¨ª sucesivamente). Si dos puntos est¨¢n a distancia uno, caer¨¢n en hex¨¢gonos distintos de distinto color" (no necesariamente adyacentes)..

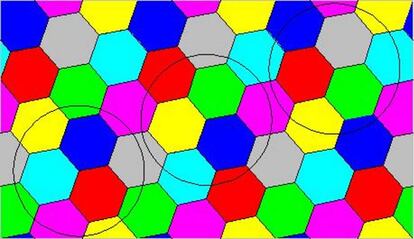
Est¨¢ claro entonces que siete es la cota m¨¢xima para el problema, pero, ?hay una m¨ªnima? Para ver que ha de ser al menos cuatro, bastar¨ªa con encontrar una configuraci¨®n de cuatro puntos que est¨¦n todos a distancia uno del resto (que, por tanto, no podr¨ªan colorearse con solo tres colores). Pero el caso es que no existe: cuatro puntos que disten todos uno entre s¨ª forman los v¨¦rtices de un tetraedro regular, cuyos v¨¦rtices no est¨¢n sobre el mismo plano. Sin embargo, son conocidas algunas configuraciones de puntos que necesitan cuatro colores (es imposible hacerlo con tres). As¨ª sucede como los siete puntos del llamado ¡°huso de Moser¡± que son los se?alados en la siguiente imagen:

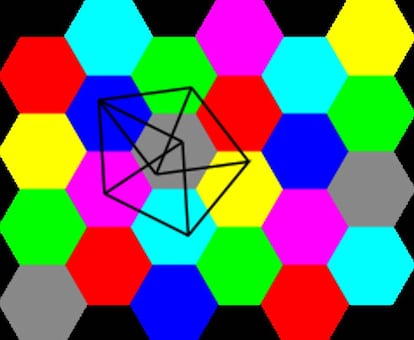
En 1961 los hermanos William y Leo Moser dieron esa configuraci¨®n, y desde entonces no se hab¨ªa avanzado nada en el problema. Ahora Aubrey de Grey ha dado una configuraci¨®n de puntos tales que necesitan al menos cinco colores para ser coloreados, es imposible hacerlo con cuatro. Aunque el ejemplo dado por Grey contiene 1581 puntos, el m¨¦todo para construirlo es descriptivo y no es excesivamente complicado. En los ¨²ltimos d¨ªas se ha conseguido rebajar la configuraci¨®n hasta los 633 v¨¦rtices, a trav¨¦s de un proyecto de Polymath (proyectos colaborativos en los que trabajan cientos de matem¨¢ticos a trav¨¦s de una p¨¢gina web), creado por el propio de Grey.

Con este avance, ya sabemos que para poder colorear cualquier grafo har¨¢n falta cinco, seis o siete colores diferentes. Para zanjar el problema existen dos posibilidades: que usando ideas parecidas a las de De Grey se encuentren estructuras con gran cantidad de puntos que requieran muchos colores para ser coloreadas (¨¦l ha encontrado una que necesita cinco, se tratar¨ªa de encontrar otra con seis y, para solucionar el problema, necesitar¨ªamos otra con siete). As¨ª sabr¨ªamos que el n¨²mero necesario para colorear el plano de forma que cualquier par de puntos a distancia uno tengan diferente color es siete. Si, por el contrario, la soluci¨®n no es siete, es posible que sean necesarias nuevas t¨¦cnicas totalmente desconocidas hasta el momento, porque no bastar¨ªa con ir descartando opciones con contraejemplos, sino dar un razonamiento general.

Alberto M¨¢rquez es Catedr¨¢tico de Matem¨¢tica Aplicada de la Universidad de Sevilla y ?gata Tim¨®n es responsable de Comunicaci¨®n y Divulgaci¨®n en el ICMAT

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.