Un matem¨¢tico ruso desmiente una conjetura con m¨¢s de medio siglo de vida

Casi coincidiendo con su 30 cumplea?os (fue el pasado 3 de junio), el nombre de Yaroslav Shitov ha aparecido en buena parte de la prensa mundial. Este matem¨¢tico ruso ha probado que una conjetura con m¨¢s de medio siglo de vida sobre un problema de teor¨ªa de grafos es falsa, dando un contraejemplo, es decir, aportando un caso en el que no se cumple lo que la conjetura predec¨ªa que suced¨ªa siempre.

Los grafos son una de las estructuras m¨¢s simples y, a la vez, m¨¢s vers¨¢tiles de las matem¨¢ticas, con gran cantidad de aplicaciones (desde el dise?o de redes de comunicaciones a la distribuci¨®n de mercanc¨ªas y planificaci¨®n de la producci¨®n). Los componen dos tipos de elementos: v¨¦rtices o puntos, y aristas, que son parejas de puntos. Se suele representar un grafo por un dibujo en el que los v¨¦rtices son puntos en el plano y las aristas son segmentos que los unen.

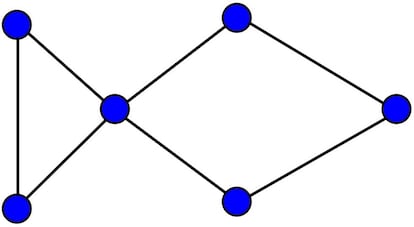
Uno de los problemas m¨¢s estudiados en este campo trata de encontrar el m¨ªnimo n¨²mero de colores que se pueden asignar a los v¨¦rtices de tal forma que no existan dos con el mismo color que est¨¦n unidos por una arista.

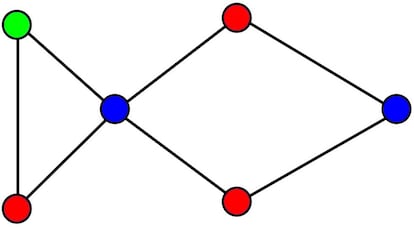
El problema de coloreado de grafos se suele usar para clasificar objetos o para optimizar procesos. Por ejemplo, los v¨¦rtices pueden ser tareas a completar por un conjunto de trabajadores y una arista entre dos v¨¦rtices indica que esas dos tareas las ha de realizar el mismo trabajador, o que son incompatibles por alguna otra raz¨®n. Si cada color representa una franja de tiempo, podemos asegurar que las tareas representadas en el grafo anterior necesitan al menos tres franjas de tiempo para completarse.

La historia del coloreado de grafos es muy extensa y se puede remontar a mediados del siglo XIX, cuando Francis Guthrie (o su hermano) conjetur¨® que cualquier grafo que se pueda dibujar en el plano de forma que dos aristas distintas no se crucen, salvo en un v¨¦rtice com¨²n, se puede colorear siempre con cuatro colores o menos. Este es el llamado problema del mapa de los cuatro colores, que fue resuelto definitivamente por los matem¨¢ticos Kenneth Appel y Wolfgang Hanken en 1976, m¨¢s de 125 a?os despu¨¦s.

Aunque parezcan juegos de ni?os, los problemas de coloraci¨®n pueden ser endiabladamente complicados: determinar si un grafo puede ser coloreado con menos de una cantidad fija de colores es un problema NP-completo. Esto significa que si nos dan una posible coloraci¨®n, podemos comprobar tanto si tiene menos de los colores que nos piden y si es v¨¢lida, pero es tremendamente dif¨ªcil encontrar esa coloraci¨®n si no nos la dan. Por tanto, si encontramos un algoritmo que resuelva de forma eficiente el problema de colorear grafos (con una cantidad de operaciones menor que una cantidad relacionada con el n¨²mero de v¨¦rtices del grafo), podemos ir al instituto Clay y reclamar un mill¨®n de d¨®lares, porque habremos demostrado que P es igual a NP, y con ello uno de los c¨¦lebres problemas del milenio cuya resoluci¨®n lleva asignada ese premio. Si alguno de los lectores tiene el algoritmo pero no entiende por qu¨¦ implica que P es igual a NP, los autores de este art¨ªculo se brindan a aclarar las dudas. Compartiendo parte del premio, claro est¨¢.

Dada la complicaci¨®n de los problemas de coloreado, un avance ser¨ªa saber cu¨¢l es el m¨ªnimo n¨²mero de colores necesarios para algunos tipos de grafos. Y en este contexto aparece la conjetura de Hedetniemi. En 1966 Stephen Hedetniemi conjetur¨® en su tesis doctoral que dados dos grafos G y H, el n¨²mero de colores necesario para colorear el grafo producto tensorial GXH es el menor de los colores necesarios para colorear G y H. Este grafo se obtiene combinando de cierta forma los v¨¦rtices y aristas de G y H.

Esto se cumpl¨ªa para todos los ejemplos que se hab¨ªan encontrado hasta hace un mes, pero nadie hab¨ªa conseguido demostrarlo formalmente. Y por una buena raz¨®n: porque es falso. El joven matem¨¢tico ruso Shitov ha encontrado dos grafos G y H tales que su producto tensorial necesita menos colores que los requeridos para colorear tanto G como H, demostrando as¨ª que la conjetura de Hedetniemi es falsa.

Los ejemplos G y H de Shitov son grafos enormes: es posible que G tenga 2²⁰⁰ v¨¦rtices, lo cual es un n¨²mero inmenso, de un orden de magnitud cercano al n¨²mero de part¨ªculas elementales que podemos encontrar en todo el universo visible. Pero H es a¨²n mayor, mucho mayor, con m¨¢s de 2²⁰⁰⁰⁰ v¨¦rtices. De hecho no los construye expl¨ªcitamente en su corto art¨ªculo (dos p¨¢ginas y media). Pero demuestra que existen bas¨¢ndose en propiedades conocidas, con lo que queda resuelto el problema.

Alberto M¨¢rquez es catedr¨¢tico de Matem¨¢tica Aplicada de la Universidad de Sevilla

?gata A. Tim¨®n G Longoria es responsable de Comunicaci¨®n y Divulgaci¨®n en el Instituto de Ciencias Matem¨¢ticas (ICMAT)

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinada por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter