El tri¨¢ngulo de Pascal

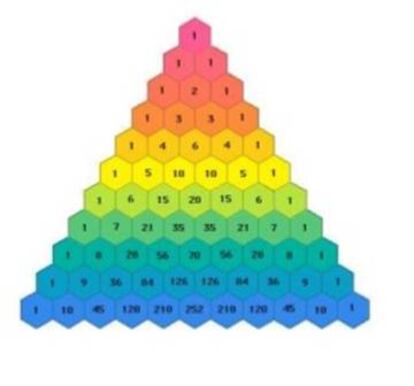
Nos pregunt¨¢bamos la semana pasada si se puede establecer alguna relaci¨®n entre el tri¨¢ngulo de Sierpinski y el tri¨¢ngulo de Pascal. Como ha se?alado Guillermo Navas, coloreando los n¨²meros impares del tri¨¢ngulo de Pascal y dejando en blanco los pares, se obtiene un tri¨¢ngulo de Sierpinski (ver comentario 144 de la entrega anterior).

En cuanto a la superficie (S) del copo de nieve de Koch, es f¨¢cil ver que, si tomamos como unidad el ¨¢rea del tri¨¢ngulo inicial, las sucesivas adiciones de ¨¢reas dan lugar a la serie siguiente:

S = 1 + 1/3 + 2²/3³ + 2⁴/3⁵ + 2⁶/3⁷¡­

Podemos hallar S mediante un sencillo y elegante ¡°truco¡±, restando 1 a ambos miembros de la igualdad y luego multiplic¨¢ndolos por 4/9:

M¨¢s informaci¨®n

N¨²meros normales

Piensa un n¨²mero

4/9 (S ¨C 1) = 2²/3³ + 2⁴/3⁵ + 2⁶/3⁷ + 2⁸/3⁹¡­ = S ¨C 1 ¨C 1/3

4S ¨C 4 = 9S ¨C 9 ¨C 3

5S = 8

S = 8/5 = 1,6

El per¨ªmetro del copo, sin embargo, crece indefinidamente, puesto que se trata de una progresi¨®n geom¨¦trica creciente: en cada paso, cada lado de la configuraci¨®n anterior se multiplica por 4/3. Nos encontramos, pues, con una sorprendente figura de ¨¢rea finita y per¨ªmetro infinito.

El tri¨¢ngulo del tartamudo

Hemos visto la relaci¨®n del tri¨¢ngulo de Sierpinski con el de Pascal. Recordemos la sencilla construcci¨®n de este ¨²ltimo: en su primera fila hay un ¨²nico 1, en la segunda dos 1, en la tercera dos 1 con un 2 entre ellos¡­ En cada fila, cada n¨²mero es la suma de los que tiene justo encima (solo uno -un 1- en el caso de los extremos y dos en el de los dem¨¢s). Estos n¨²meros son los coeficientes del desarrollo de las sucesivas potencias de una suma de dos sumandos: (a + b)ⁿ, o sea, del binomio de Newton:

(a + b)⁰ = 1

(a + b)¹ = 1a + 1b

(a + b)² = 1a² + 2ab + 1b²

(a + b)³ = 1a³ + 3a²b + 3ab² + b³

El tri¨¢ngulo de Pascal se conoce tambi¨¦n como tri¨¢ngulo de Tartaglia, en honor del matem¨¢tico italiano Niccol¨° Fontana, apodado Tartaglia por su tartamudez, que lo estudi¨® antes que Pascal, aunque menos a fondo. Pero en realidad tampoco fue ¨¦l el primero, pues en India se conoc¨ªa este tri¨¢ngulo num¨¦rico desde al menos el siglo X, y en Persia lo estudi¨®, entre otros, el gran matem¨¢tico y poeta Omar Jayam.

La sencilla configuraci¨®n de este tri¨¢ngulo num¨¦rico encierra interesantes propiedades. Podemos relacionarlo con las potencias de 2, con la sucesi¨®n de Fibonacci e incluso con los escurridizos n¨²meros primos. ?De qu¨¦ maneras? ?Qu¨¦ otras propiedades y posibles generalizaciones ves en ¨¦l, sagaz lector(a)?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.