Una salvaje horda de peones
Lord Dunsany, el maestro de Lovecraft, invent¨® una variante del ajedrez en la que el rey y su corte son atacados por una horda de peones

En relaci¨®n con los juegos de estrategia segura, a los que alud¨ªamos la semana pasada al hablar del Nim, Jes¨²s Catal¨¢n plantea la siguiente pregunta:
¡°Mencionas las damas; sabiendo que son menos fichas y m¨¢s limitados sus movimientos, ?es un juego de estrategia segura?¡±.
Pues s¨ª, al menos para la variante de 12 fichas por bando, se demostr¨® en 2007 que si ambos jugadores siguen en cada momento la estrategia ¨®ptima, la partida termina necesariamente en tablas. Para la variante de 20 fichas por bando, que permite un n¨²mero de combinaciones much¨ªsimo mayor, no est¨¢ demostrado (que yo sepa), aunque, por extrapolaci¨®n, algunos dan por supuesto que la ¡°partida perfecta¡± tambi¨¦n terminar¨¢ en tablas.
En cuanto al problema de antichess, podr¨ªa parecer que si el pe¨®n negro se convierte en dama al coronar, luego podr¨¢ ponerse f¨¢cilmente a tiro de alguna pieza blanca para forzar su captura (ya que en esta modalidad es obligatorio comer siempre que se pueda); pero, como se?ala Salva Fuster:
¡°En el problema propuesto, promocionar a una dama o a una torre ser¨ªa un error, pues las jugadas de las piezas blancas podr¨ªan ser las siguientes:
Dg6
a4
a5
c4
c5
h5
Y si las piezas negras promocionan a un alfil, tampoco podr¨ªan ganar, pues las blancas podr¨ªan conseguir promocionar su pe¨®n a6 a un alfil de casilla blanca. Yo dir¨ªa que si las negras promocionan a un rey, las blancas pierden¡±.
Efectivamente, esa es la promoci¨®n que da la victoria a las negras, que es la que ¨²nicamente es posible en la variante pierde-gana, es decir, la conversi¨®n del pe¨®n coronado (nunca mejor dicho) en rey.

Ahora juegan las blancas y las negras ganan (es decir, obligan a las blancas a comer al rey) en 17 jugadas. ?Puedes reconstruir este interesante final? Por cierto, la posici¨®n est¨¢ tomada de una partida real de antichess en la variante ¡°solo peones¡±, en la que, como su nombre indica, al comienzo de la partida se retiran del tablero todas las piezas menos los peones.
El ajedrez de Dunsany
El antichess es una de las variantes del ajedrez que puedes encontrar en la web Lichess, junto al ajedrez at¨®mico, el ajedrez aleatorio de Fischer (en el que la posici¨®n inicial de las piezas se determina por sorteo en cada partida) o el Horda, que es una variante del ajedrez de Dunsany.
Lord Dunsany, adem¨¢s de escribir fascinantes relatos de fantas¨ªa y terror (Lovecraft lo consideraba su maestro y Borges lo admiraba), invent¨® una variante asim¨¦trica del ajedrez en la que una ¡°horda¡± de 32 peones (de ah¨ª el nombre con el que tambi¨¦n se conoce esta modalidad) se enfrenta a las 16 piezas convencionales. La horda gana dando jaque mate al rey, y el bando convencional gana capturando todos los peones contrarios antes de que se agoten sus posibilidades de movimiento. En el caso de que el jugador de la horda no pueda mover porque todos sus peones est¨¢n inmovilizados, la partida se considera tablas.

Hay una variante con las casillas de dama y rey de la horda vac¨ªas y un par de peones encabezando la formaci¨®n desde las casillas centrales de la quinta fila (esta es la variante m¨¢s com¨²n en Lichess y la que m¨¢s espec¨ªficamente se denomina Horda), y otra con 36 peones en vez de 32.
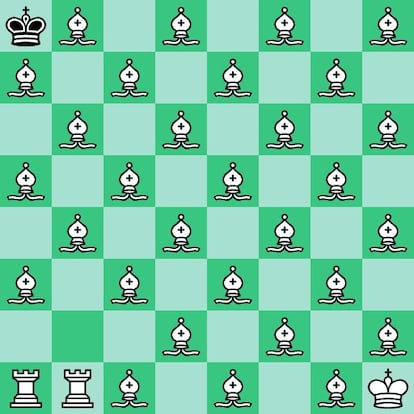
Y puestos a recargar el tablero con piezas excesivas, he aqu¨ª un curioso problema en el que las blancas tienen que dar jaque mate al solitario rey negro en un tablero atestado de alfiles blancos, todos sobre casilla negra. ?Crees que es posible?
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
Sobre la firma



































































