?La dama o el tigre?

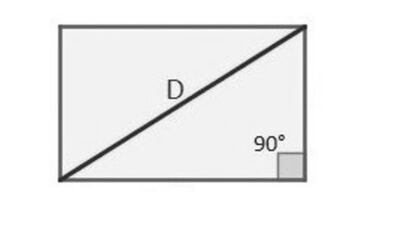
Al intentar demostrar que los n¨²meros irracionales son numerables, George Cantor encontr¨® la demostraci¨®n de que no lo son. Salvando las (enormes) distancias, al intentar construir el hipot¨¦tico ¡°tetraedro egipcio¡± de la semana pasada, encontr¨¦ una sencilla y muy visual/evidente demostraci¨®n de su imposibilidad. En efecto, la forma m¨¢s simple de construir (mentalmente) dicho tetraedro ser¨ªa partir de un rect¨¢ngulo de 3x4 y doblarlo por una diagonal hasta que los v¨¦rtices opuestos estuvieran a una distancia de 5 unidades. Pero la cuesti¨®n es que ya est¨¢n a esa distancia (pues la diagonal mide precisamente 5 unidades), que disminuir¨¢ al doblar el rect¨¢ngulo, lo que (de)muestra que el supuesto tetraedro egipcio es una figura plana, y que las caras de un tetraedro equi¨¦drico solo pueden ser tri¨¢ngulos acut¨¢ngulos. El imposible tetraedro egipcio es el l¨ªmite del progresivo achatamiento del tetraedro equi¨¦drico a medida que uno de los ¨¢ngulos de sus caras tiende a 90?.

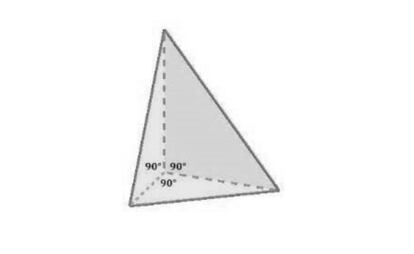
El que s¨ª existe es el tetraedro trirrect¨¢ngular o tetraedro trirrect¨¢ngulo, que es aquel en el que los tres ¨¢ngulos de las caras que convergen en un v¨¦rtice son rectos. Las tres aristas que convergen en ese v¨¦rtice son, pues, los catetos de dichas caras, que obviamente son tri¨¢ngulos rect¨¢ngulos, y las tres hipotenusas son los lados de la cara mayor del tetraedro trirrect¨¢ngulo, que se llama base (independientemente de la posici¨®n del tetraedro). ?Puedes hallar la altura perpendicular a la base del tetraedro trirrect¨¢ngulo en funci¨®n de sus tres catetos? ?Y el volumen? ?Y el ¨¢rea de la base?

Y como colof¨®n, un elegante problema propuesto por Salva Fuster: dado un tetraedro equiedro cuyas caras son tri¨¢ngulos is¨®sceles, encontrar el volumen m¨ªnimo de la esfera que lo contiene, sabiendo que el volumen del tetraedro es un n¨²mero entero.

Decisiones problem¨¢ticas

En entregas recientes hemos visto algunos problemas y paradojas relacionados con la teor¨ªa de la decisi¨®n (ver La paradoja de Elsberg y La paradoja de Simpson), por lo que no est¨¢ de m¨¢s recordar el famoso relato de Frank R. Stockton ?La dama o el tigre?, publicado en 1882 y desde entonces citado a menudo al hablar de la toma de decisiones y del libre albedr¨ªo. Muy resumida, la historia es la siguiente:

El protagonista tiene que elegir entre dos puertas: tras una de ellas hay un tigre hambriento y tras la otra una hermosa joven con la que tendr¨¢ que casarse. La amante del protagonista sabe tras qu¨¦ puerta est¨¢ el tigre. No quiere ver a su amado devorado por la fiera, pero tampoco soporta la idea de verlo casado con su bella rival, y ¨¦l lo sabe. Ella le indica con una se?a qu¨¦ puerta debe abrir. ?Qu¨¦ hace ¨¦l?

Inspir¨¢ndose en este inquietante relato, Raymond Smullyan, el gran maestro contempor¨¢neo de los acertijos l¨®gicos, public¨® cien a?os despu¨¦s -en 1982- un delicioso libro con el mismo t¨ªtulo, en el que tienes que superar un mont¨®n de pruebas tan peligrosas como las siguientes:

Hay dos puertas. En la I hay un letrero que dice: ¡°Al menos tras una de estas dos puertas hay una dama¡±. En la II hay un letrero que dice: ¡°Hay un tigre tras la otra puerta¡±. Sabiendo que o bien los dos letreros dicen la verdad o bien los dos mienten, ?qu¨¦ puerta elegir¨ªas?

Hay tres puertas. El letrero de la I dice: ¡°Tras esta puerta hay un tigre¡±. El de la II dice: ¡°Tras esta puerta hay una dama¡±. El de la III dice: ¡°Tras la puerta II hay un tigre¡±. Sabiendo que a lo sumo uno de los tres letreros dice la verdad, ?qu¨¦ puerta elegir¨ªas?

En ambos casos se supone que prefieres la dama al tigre.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.