GRAFOS
K?nigsberg, Euler y dibujos en un solo trazo
Te mostramos cu¨¢ndo y c¨®mo puedes recorrer todas las l¨ªneas de un trabajo sin repetir ninguna
Curiosidades num¨¦ricas
El enigma del 196
El simple proceso de invertir y sumar nos proporciona una interesante conjetura num¨¦rica que contin¨²a sin soluci¨®n
Historia de las matem¨¢ticas
La resoluci¨®n de la c¨²bica: una historia llena de historias
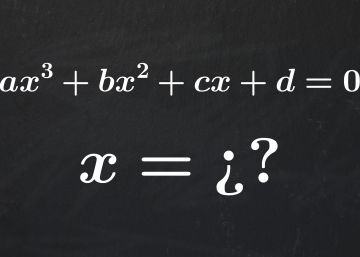
Hoy hablamos sobre la historia que rode¨® al descubrimiento del m¨¦todo para resolver ecuaciones c¨²bicas
El grafo adivinador de la letra del DNI
Te explicamos c¨®mo ¡°adivinar¡± la letra asociada a cualquier n¨²mero de DNI de una forma muy original
?Es muy dif¨ªcil (estad¨ªsticamente) no dar ni una?
?Has tenido que repetir un sorteo en el amigo invisible? Te contamos cu¨¢l es la probabilidad de que ocurra.
Pelos, saludos y palomas
El principio del palomar, un resultado muy evidente, puede dar respuesta a preguntas muy curiosas.
?Por qu¨¦ las antenas parab¨®licas son parab¨®licas?
Su forma no es ni mucho menos casual, y tiene explicaci¨®n matem¨¢tica
El Tangram, Bolyai-Gerwien y la cuadratura del c¨ªrculo
C¨®mo jugar ¡°matem¨¢ticamente¡± con piezas para formar distintos pol¨ªgonos
La Regla del Fin de los D¨ªas
Un sencillo m¨¦todo para calcular en qu¨¦ d¨ªa de la semana cae una fecha cualquiera
Fermat y los pol¨ªgonos regulares
La inesperada relaci¨®n entre unos primos muy especiales y los pol¨ªgonos regulares
Una f¨®rmula para dominarlos a todos (los poliedros convexos)
Una de las m¨¢s maravillosas aportaciones de Euler a la geometr¨ªa
(Creemos que) Todos los n¨²meros est¨¢n en Pi
?Podemos encontrar en Pi cualquier n¨²mero que se nos ocurra? Creemos que s¨ª, pero no lo sabemos con seguridad.
Lo m¨¢s irracional de los racionales
Cuando el infinito hace acto de presencia, hasta las propiedades m¨¢s b¨¢sicas pueden dejar de cumplirse
Los tesoros matem¨¢ticos que esconde el tri¨¢ngulo de Pascal
Una interesante recopilaci¨®n de algunas de las curiosidades matem¨¢ticas que se pueden encontrar en el tri¨¢ngulo de Pascal
?Por qu¨¦ no se puede cuadrar un c¨ªrculo?
Explicamos por qu¨¦ es imposible, matem¨¢ticamente, realizar la cuadratura del c¨ªrculo
Manhattan, distancias y ¡°el juicio de Pit¨¢goras¡±
Algo tan sencillo como calcular la distancia entre dos puntos puede ser determinante en un juicio.
La paradoja de Bertrand: tri¨¢ngulos, circunferencias y probabilidad
El simple hecho de comparar la longitud de dos segmentos puede llevarnos a una paradoja de dif¨ªcil soluci¨®n.
Amazing Grace
La inform¨¢tica del mundo de los negocios le debe mucho a la matem¨¢tica Grace Murray Hopper
En busca de la caja perfecta
Un interesante ejemplo de problema sencillo de plantear y complicado de resolver.
La circunferencia de Feuerbach o por qu¨¦ me encantan los tri¨¢ngulos
La geometr¨ªa plana, a pesar de su aparente sencillez, esconde aut¨¦nticas maravillas. Y, en concreto, la geometr¨ªa del tri¨¢ngulo es tremendamente rica en sorpresas geom¨¦tricas, hechos inesperados que la convierten en una rama de las matem¨¢ticas digna de ser estudiada en profundidad.
Cinco ¡®frikadas¡¯ matem¨¢ticas de Google
La empresa capitaneada por Larry Page y Sergey Brin ha estado, y sigue estando, en contacto constante con las matem¨¢ticas. Repasamos cinco de las ¡°frikadas¡± matem¨¢ticas m¨¢s curiosas relacionadas con Google.
Pit¨¢goras y la demostraci¨®n de los 200 TB
Las denominadas ternas pitag¨®ricas, ternas de enteros positivos que cumplen el teorema de Pit¨¢goras, han sido hace bien poco protagonistas de una de las demostraciones matem¨¢ticas m¨¢s largas que se han desarrollado hasta la fecha.
Un cuerno finito-infinito
Hace casi cuatro siglos, Torricelli descubri¨® una figura cuyas propiedades relacionan lo finito y lo infinito de una manera no conocida hasta ese momento, lo que gener¨® cierta controversia entre algunos de los principales pensadores de la ¨¦poca.
El matem¨¢tico ol¨ªmpico
No es sencillo encontrar a alguien que haya destacado en disciplinas tan distantes como las matem¨¢ticas y el deporte. Harald Bohr fue uno de los pocos (quiz¨¢s el ¨²nico) que consigui¨® alcanzar un gran nivel en ambas.
Pi, Indiana y legisladores con poco criterio
?Puede alguna ley influir directamente en hechos demostrados matem¨¢ticamente? Quiz¨¢s no deber¨ªa, pero hubo un momento de la historia en el que estuvo a punto de hacerlo.
Todos (s¨ª, TODOS) los mapas planos de la Tierra est¨¢n mal
Ninguno de los mapas planos terrestres que existen y existir¨¢n representan correctamente la superficie de nuestro planeta Tierra. La explicaci¨®n de este hecho tiene que ver, y mucho, con las matem¨¢ticas.
Y el premio al camino m¨¢s corto es para...
La curva cicloide pone en cuesti¨®n algunas verdades que cre¨ªamos establecidas "de toda la vida"
?Existe alg¨²n n¨²mero sin nombre?
Desvelamos este misterio utilizando matem¨¢ticas que, aunque no son b¨¢sicas, no ser¨¢n muy complicadas de entender