La torre y el hipercubo
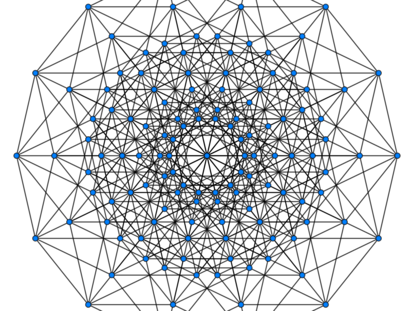
Existe una sorprendente correspondencia entre una torre de Han¨®i de ¡®n¡¯ discos y un hipercubo ¡®n-dimensional¡¯
La torre, el cubo y el tablero
Objetos matem¨¢ticos en apariencia muy distintos pueden estar relacionados de maneras sorprendentes
Por los caminos de Euler y Hamilton
A veces coinciden y a menudo se confunden, pero los caminos ¡®eulerianos¡¯ y los caminos ¡®hamiltonianos¡¯ son distintos
El tri¨¢ngulo de Jayam
El conocido como tri¨¢ngulo de Pascal o de Tartaglia es muy anterior a ambos matem¨¢ticos europeos, y fue estudiado en Persia ya en el siglo XI
2024 y los n¨²meros tetra¨¦dricos
El 2024 es el vig¨¦simo segundo n¨²mero piramidal triangular y se puede representar como un gran tetraedro de esferas apiladas
Las matem¨¢ticas del 24
La cifra del a?o 2024 no da mucho juego desde el punto de vista matem¨¢tico, pero su terminaci¨®n, el 24, no tiene desperdicio
El manicomio del doctor Brea y el profesor Pluma
Un sobrecogedor relato de Edgar Allan Poe sirve de base a un intrigante acertijo l¨®gico
?La dama o el tigre?
Hay decisiones que no parecen dudosas, como la de elegir entre un tigre hambriento y una hermosa dama, y sin embargo¡
El forjador de rayos
El matem¨¢tico alem¨¢n Charles Proteus Steinmetz, adem¨¢s de estudiar los s¨®lidos que llevan su nombre, hizo importantes contribuciones en el campo de la ingenier¨ªa el¨¦ctrica
El sistema di¨¦drico
Gaspard Monge, matem¨¢tico franc¨¦s amigo de Napole¨®n, fue el creador del sistema di¨¦drico para la representaci¨®n plana de objetos tridimensionales
N¨²meros m¨¢gicos
?Por qu¨¦ para los f¨ªsicos son ¡°m¨¢gicos¡± los n¨²meros 2, 8, 20, 28, 50, 82 y 126?
La realidad de los n¨²meros imaginarios
Descartes los denomin¨® as¨ª despectivamente, pero se convertir¨ªan en una herramienta muy real de las matem¨¢ticas
La lentitud de los fotones
?Cu¨¢nto tiempo tardan los fotones generados en el centro del Sol en alcanzar su superficie y salir al vac¨ªo?
La paradoja de Simpson
La teor¨ªa de la decisi¨®n, ligada al c¨¢lculo de probabilidades, da lugar a interesantes paradojas
El condenado y las urnas
Adem¨¢s de ser un f¨ªsico de primera fila, George Gamow fue un excelente narrador, como se aprecia en sus libros de divulgaci¨®n y de matem¨¢tica recreativa
Ascensores y algoritmos
Los problemas de optimizaci¨®n relativos al uso de ascensores dan lugar a curiosas paradojas e ingeniosos algoritmos
El ascensor de Gamow
Entre los numerosos medios de transporte que aparecen en los problemas de matem¨¢tica recreativa, no pod¨ªan faltar los ascensores
Ilustres desconocidos
Algunos n¨²meros muy importantes son conocidos y accesibles, como ¦Ð o e, pero otros, como la constante de Chaitin, son ignorados y dif¨ªciles de entender por los no matem¨¢ticos
M¨¢s n¨²meros muy interesantes
He aqu¨ª algunos candidatos a a?adir a la lista de los n¨²meros m¨¢s interesantes
Los n¨²meros m¨¢s interesantes
Todos los n¨²meros son interesantes, pero algunos lo son de una manera muy especial
Plantaci¨®n de ¨¢rboles
Seg¨²n determinadas configuraciones, plantar ¨¢rboles es un tema cl¨¢sico de los problemas de ingenio
Acertijos de autor
Muchos enigmas l¨®gicos pertenecen a la tradici¨®n oral y no se conoce su origen, pero otros son obra de prestigiosos autores
Set o no Set, esa es la cuesti¨®n
El Set es un juego de percepci¨®n visual con interesantes implicaciones matem¨¢ticas
Banquetes problem¨¢ticos
Un par de cl¨¢sicos de los problemas de ingenio abordados por matem¨¢ticos tan ilustres como Euler y Tartaglia
Humanos, m¨¢quinas y ajedrez
Las m¨¢quinas ya superan a los humanos en el ajedrez y otros juegos de estrategia; aunque al parecer no siempre consiguen batirnos
Matem¨¢ticas ancestrales
El matem¨¢tico indio Baudhayana podr¨ªa haber demostrado el teorema de Pit¨¢goras antes que los griegos
El reba?o del sol
La ecuaci¨®n diof¨¢ntica de Pell ya fue estudiada en la antig¨¹edad en relaci¨®n con el problema del ganado del Sol
?Por qu¨¦ queremos tanto a Carlo?
La relaci¨®n entre la poes¨ªa, las matem¨¢ticas y el ciberespacio es m¨¢s estrecha de lo que parece a simple vista. Carlo Frabetti nos lo descubre en su ¨²ltima novela: ¡®Terrible ¨¢ngel¡¯
Sangaku
Las tablillas de madera con acertijos geom¨¦tricos se depositaban en los templos japoneses como ofrendas votivas
Razonamiento iterativo
Algunos acertijos l¨®gicos implican pensar en lo que piensan los dem¨¢s
La paradoja de los mentirosos
Raymond Smullyan populariz¨® en la segunda mitad del siglo XX unos acertijos, inspirados en la famosa paradoja del mentiroso, protagonizados por unos personajes que siempre dec¨ªan la verdad y otros que siempre ment¨ªan
Problemas insulares
Las islas, reales o fant¨¢sticas, son escenarios frecuentes de todo tipo de acertijos l¨®gicos
La m¨¢quina del azar
¡°Los algoritmos generadores de n¨²meros aleatorios basados en congruencias num¨¦ricas en realidad producen ciclos previsibles, y solo son ¨²tiles porque nos basta con conseguir algo vagamente parecido al azar¡±, defendi¨® un cliente del bar
Primos lejanos
Entre dos n¨²meros primos consecutivos la distancia puede ser tan grande como queramos
Grandes primos
La moderna encriptaci¨®n requiere el uso de n¨²meros primos cada vez mayores; pero, de momento, no parece que vaya a fallar el suministro
Cifrado con n¨²meros primos
El producto de dos grandes n¨²meros primos es la base de eficaces m¨¦todos de encriptaci¨®n
El cifrado indescifrable
El impropiamente denominado cifrado Vigen¨¨re era tan s¨®lido que lleg¨® a considerarse indescifrable
Mensajes cifrados
Desde los or¨ªgenes de la estrategia militar hasta las actuales transacciones en red, los mensajes cifrados siempre han tenido una enorme importancia operativa
La problem¨¢tica peseta
En tiempos de la peseta hubo numerosos billetes y una gran variedad de monedas de distintas aleaciones, tama?os y valores
El problema de la mochila
Llenar una mochila de forma ¨®ptima puede ser un problema menos sencillo de lo que parece