Estrategia segura
?Puede haber en el ajedrez una estrategia que garantice la victoria de las negras?
El molino
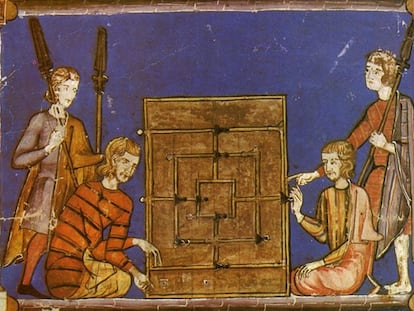
El molino (tambi¨¦n conocido como Morris o Nueve hombres de Morris) es uno de los m¨¢s populares juegos de tablero derivados del alquerque
El alquerque
El alquerque es un milenario juego de tablero que dio lugar a numerosas variantes, como el molino o las damas
Matem¨¢ticas de ¡®saloon¡¯
En una partida de cartas el c¨¢lculo de probabilidades puede marcar la diferencia entre ganar y perder
Dodomin¨®s
El p¨¢jaro dodo de ¡®Alicia en el Pa¨ªs de las Maravillas¡¯ representa al propio Carroll, que tartamudeaba al decir su apellido: Do¡ Do¡ Dodgson
El vers¨¢til ladrillo
El orto¨¦drico ladrillo une a su inter¨¦s como cuerpo geom¨¦trico sus m¨²ltiples aplicaciones como objeto material
Cajas
Los contenedores orto¨¦dricos, como las cajas de cart¨®n y los tetrabriks, dan lugar a interesantes problemas de optimizaci¨®n
Grafos
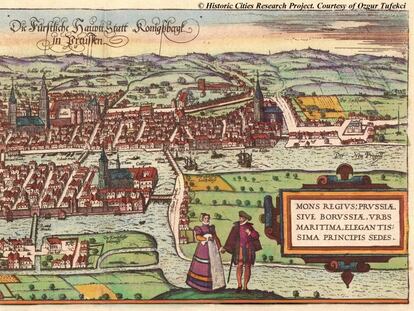
Euler introdujo la teor¨ªa de grafos al analizar el famoso problema de los puentes de K?nigsberg
Sucesiones no num¨¦ricas
La naturaleza, la historia y el lenguaje mismo ofrecen numerosos ejemplos de secuencias no num¨¦ricas
Torneos y combinaciones
Los torneos y otras competiciones eliminatorias plantean problemas combinatorios no siempre f¨¢ciles de resolver
Voracidad y optimizaci¨®n
La voracidad es tambi¨¦n un concepto inform¨¢tico y una forma de optimizar resultados
Los renos de Pap¨¢ Noel
Los renos del trineo de Pap¨¢ Noel y sus itinerarios se prestan a interesantes consideraciones combinatorias
Teselaciones posibles e imposibles
Los domin¨®s y tromin¨®s plantean interesantes problemas de teselaci¨®n del tablero de ajedrez y otras superficies acotadas
Sin l¨ªneas de fractura
Solomon W. Golomb y Martin Gardner estudiaron los mosaicos de poliomin¨®s sin l¨ªneas de fractura
Particiones y poliomin¨®s
Las particiones de los n¨²meros naturales en sumandos fueron estudiadas por Hardy y Ramanujan a principios del siglo pasado
Particiones num¨¦ricas
Las particiones de n¨²meros naturales en sumandos constituyen un importante cap¨ªtulo de las matem¨¢ticas discretas
Particiones y repartos
No siempre es f¨¢cil repartir de forma equitativa y a gusto de todos, o tan siquiera saber cu¨¢ntas partes se pueden obtener
Problemas imposibles
Hay problemas que parecen imposibles de resolver, como algunos de los que aparecen en los libros de Clifford Pickover, y sin embargo¡
Las siete unidades b¨¢sicas
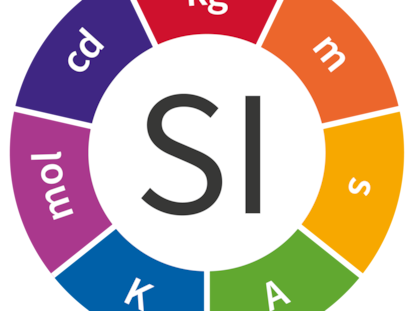
El Sistema Internacional define siete unidades b¨¢sicas correspondientes a otras tantas magnitudes f¨ªsicas fundamentales
Masa, peso y cantidad de sustancia
No hay que confundir la masa con el peso ni con la cantidad de sustancia de un objeto f¨ªsico
Logaritmos
El matem¨¢tico ingl¨¦s Henry Briggs propuso los logaritmos decimales como alternativa a los neperianos
El ¨¢baco neperiano
Adem¨¢s de inventar los logaritmos, John Napier ide¨® un ingenioso ¨¢baco para simplificar las operaciones aritm¨¦ticas
Referente universal
El agua no solo es el disolvente universal, sino tambi¨¦n un referente para los sistemas de unidades
Paradojas del calor y el fr¨ªo
?C¨®mo es posible que los ventiladores nos refresquen, cuando en realidad calientan el aire al moverlo?
Celsius y Fahrenheit
?Puede haber confusi¨®n entre los grados cent¨ªgrados, Celsius y Fahrenheit?
La conversi¨®n de la energ¨ªa
Hasta mediados del siglo XIX no se comprendi¨® que el calor es una forma de energ¨ªa
La conservaci¨®n de la energ¨ªa
La revoluci¨®n relativista oblig¨® a reformular la ley de la conservaci¨®n de la energ¨ªa
El plano inclinado de Galileo
En realidad, los experimentos de Galileo ten¨ªan m¨¢s que ver con planos inclinados que con torres inclinadas
Galileo contra Arist¨®teles
Galileo demostr¨® que Arist¨®teles se equivocaba al pensar que los cuerpos pesados ca¨ªan m¨¢s deprisa que los ligeros
El p¨¦ndulo de Foucault
?Cu¨¢nto tardar¨ªa en efectuar una oscilaci¨®n completa un p¨¦ndulo con un hilo de 100 metros?
M¨¢s enigmas de autor (y autora)
Cuatro acertijos veraniegos de tres grandes maestros y una gran maestra de la matem¨¢tica recreativa
Enigmas de autor
Muchos acertijos l¨®gico-matem¨¢ticos son an¨®nimos, como los chistes, pero otros proceden de ilustres autores
Rompecabezas geom¨¦tricos
Desde el tradicional tangram hasta los modernos ¡®IQ puzzles¡¯, los rompecabezas geom¨¦tricos han merecido la atenci¨®n de prestigiosos cient¨ªficos
N¨²meros romances
No solo seguimos utilizando los n¨²meros romanos, sino que a¨²n pueden depararnos algunas sorpresas
Gravedad problem¨¢tica
Puestos a fantasear, ?qu¨¦ pasar¨ªa si la gravedad fuera distinta de como la conocemos?
Las supermemeces de Superman
Adem¨¢s de ser inveros¨ªmiles, a menudo las haza?as de Superman violan las leyes de la f¨ªsica¡ y de la l¨®gica
Viajes problem¨¢ticos
En las novelas de Jules Verne encontramos interesantes ejemplos de problemas relacionados con los viajes y los viajeros
Cajas problem¨¢ticas
¡®El mercader de Venecia¡¯ de Shakespeare inspir¨® algunos de los acertijos l¨®gicos del maestro Raymond Smullyan
Empaquetamiento compacto
El astr¨®nomo y matem¨¢tico ingl¨¦s Thomas Harriot fue el primero en calcular el n¨²mero de balas de ca?¨®n de un apilamiento piramidal
Cajas enigm¨¢ticas
Los problemas probabil¨ªsticos y geom¨¦tricos con cajas constituyen un inagotable fil¨®n de la matem¨¢tica recreativa