De urnas y pretendientes
?Qu¨¦ tiene que ver el contenido de una urna con la elecci¨®n de un pretendiente?
El problema del bar ¡®El Farol¡¯
Si el bar no est¨¢ muy lleno, es un lugar agradable; si est¨¢ atestado, no; pero no puedes saber de antemano cu¨¢nta gente ir¨¢. ?C¨®mo tomar una decisi¨®n?
Una salvaje horda de peones
Lord Dunsany, el maestro de Lovecraft, invent¨® una variante del ajedrez en la que el rey y su corte son atacados por una horda de peones
El que pierde, gana
?Sab¨ªas que hay variantes del ajedrez en las que los perdedores se convierten en ganadores?
Si te lo llevas, pierdes
?Puedes superar en ingenio a los ensimismados protagonistas de ¡®El a?o pasado en Marienbad¡¯?
El efecto Will Rogers: del chiste a la paradoja
Si una persona viaja de un estado a otro, ?puede crecer la inteligencia media en ambos estados?
El principio de Pareto o por qu¨¦ el 20% de los jugadores anotan el 80% de los tantos
El economista y fil¨®sofo italiano Vilfredo Pareto propuso a finales del siglo XIX un principio que establece, de forma general, la regla del 80/20
Proporciones desconcertantes
?En qu¨¦ proporci¨®n est¨¢n las respectivas poblaciones de la primera ciudad en n¨²mero de habitantes y la segunda, la tercera, la cuarta¡?
Los desconcertantes n¨²meros an¨®malos
Las primeras p¨¢ginas de las viejas tablas de logaritmos est¨¢n m¨¢s usadas que las siguientes, ?a qu¨¦ crees que se debe?
La s¨¦ptima operaci¨®n
?Sabes por qu¨¦ la suma de logaritmos equivale a una multiplicaci¨®n?
Los siete mosqueteros
Al igual que los tres mosqueteros eran cuatro, las cuatro operaciones son siete. ?Puedes nombrarlas todas?
Los bueyes de Newton y el reloj de Einstein
?Puedes resolver tan deprisa como Einstein el problema del reloj blando de agujas deformables?
Tolst¨®i y los segadores diligentes
?Te atreves a emular al autor de ¡®Guerra y paz¡¯ en la resoluci¨®n de un enrevesado problema agr¨ªcola?
Los Perelman: ?C¨®mo crees que es la sombra de un avi¨®n?
?Es mayor, menor o igual que el propio avi¨®n?
?Qu¨¦ es un conjunto?
Tenemos muy claro qu¨¦ es un conjunto de cosas cualesquiera¡ ?o no est¨¢ tan claro? ?C¨®mo definir¨ªas un conjunto?
?Qu¨¦ es una curva?
Seguro que sabes ¡ªo crees saber¡ª qu¨¦ es una curva, pero ?puedes definirla con precisi¨®n?
Sobres, puentes, p¨¢jaros y peces
?Pesar¨¢ menos la jaula si el pajarito abandona el balanc¨ªn y revolotea por su interior?
Puentes problem¨¢ticos
?Podr¨ªas dibujar un croquis de los cinco puentes de Kaliningrado a partir de la informaci¨®n contenida en este art¨ªculo?
Mec¨¢nica popular: el misterio del tap¨®n de corcho
?C¨®mo adaptar¨ªas un tap¨®n de corcho para poder usarlo con una botella cuya boca tiene un di¨¢metro inferior al del tap¨®n?
Hundido en el fango
?C¨®mo liberar¨ªas un coche atrapado en el barro si solo dispusieras de una cuerda larga?
?En qu¨¦ momento de su vaciado ser¨¢ m¨¢s estable una lata de cerveza?
Es posible determinar en qu¨¦ momento de su vertido progresivo estar¨¢ m¨¢s equilibrado el recipiente
Extra?as coincidencias
?Cu¨¢l es la probabilidad de que, en un grupo de siete personas, dos celebren su cumplea?os la misma semana?
Borges y el infinito
?Puedes imaginar un laberinto sin fin? ?Y uno del que se saliera girando siempre hacia la izquierda?
Borges deconstruido
En su novela ¡®Ada o el ardor¡¯, Vladimir Nabokov convierte a Borges en Osberg. ?Puedes revertir la deconstrucci¨®n y devolverle su nombre al escritor argentino?
El arte de doblar mapas
?De cu¨¢ntas maneras distintas puedes doblar un sencillo mapa con dos dobleces verticales y uno horizontal?
El arte de doblar papel
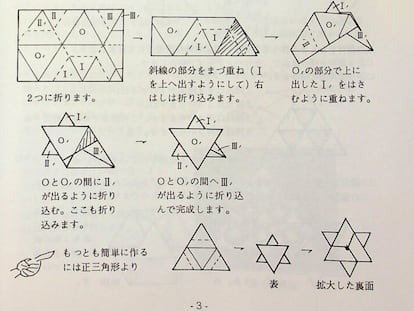
?Cu¨¢ntas veces y de cu¨¢ntas maneras distintas puedes doblar una hoja de papel?
Pol¨ªgonos sagrados y estrellas malditas
?Puedes dibujar un pent¨¢gono regular sin utilizar una regla graduada? ?Y un heptadec¨¢gono?
Descartes vs Fermat: el combate del siglo XVII
Los dos pesos pesados de las matem¨¢ticas francesas se enfrentaron en el ring de las coordenadas¡ ?cartesianas?
El beso preciso
El qu¨ªmico ingl¨¦s Frederick Soddy redescubri¨® el teorema de Descartes y lo convirti¨® en un poema er¨®tico
La mosca de Descartes
El vuelo de una mosca le inspir¨® a Descartes las coordenadas que llevan su nombre
Haciendo juegos de manos con los n¨²meros
Nuestra base num¨¦rica es decimal debido a una disposici¨®n gen¨¦tica, a un capricho biol¨®gico que nos lleva a enumerar cosas con los dedos
La elipse de Steiner
Adem¨¢s de sus contribuciones a la teor¨ªa de dise?os combinatorios, Jakob Steiner fue uno de los m¨¢s grandes ge¨®metras de todos los tiempos
Poes¨ªa y matem¨¢ticas
En la singular estructura de la sextina confluyen la poes¨ªa y las matem¨¢ticas
Combinatoria y autorreferencia
Las combinaciones de letras, personas u otros elementos y la autorreferencia son inagotables fuentes de problemas y paradojas
La sopa (de letras) primordial
Al igual que la vida, las palabras surgen de una sopa (de letras) primordial y una combinatoria inagotable
La torre y el tri¨¢ngulo
Mediante la teor¨ªa de grafos, la torre de Han¨®i tambi¨¦n se relaciona con el tri¨¢ngulo de Sierpinski
La torre y el hipercubo
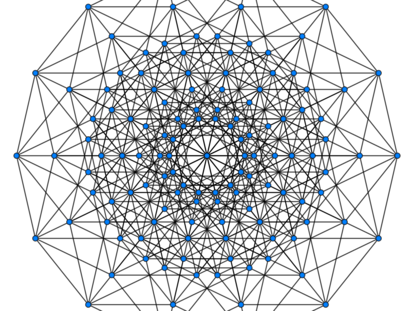
Existe una sorprendente correspondencia entre una torre de Han¨®i de ¡®n¡¯ discos y un hipercubo ¡®n-dimensional¡¯
La torre, el cubo y el tablero
Objetos matem¨¢ticos en apariencia muy distintos pueden estar relacionados de maneras sorprendentes
Por los caminos de Euler y Hamilton
A veces coinciden y a menudo se confunden, pero los caminos ¡®eulerianos¡¯ y los caminos ¡®hamiltonianos¡¯ son distintos
El tri¨¢ngulo de Jayam
El conocido como tri¨¢ngulo de Pascal o de Tartaglia es muy anterior a ambos matem¨¢ticos europeos, y fue estudiado en Persia ya en el siglo XI